


题目描述
给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发,每一步只能往 下 或者往 右 ,你想要到达终点 (m - 1, n - 1) 。
请你返回路径和能被 k 整除的路径数目,由于答案可能很大,返回答案对 109 + 7 取余 的结果。
示例 1:
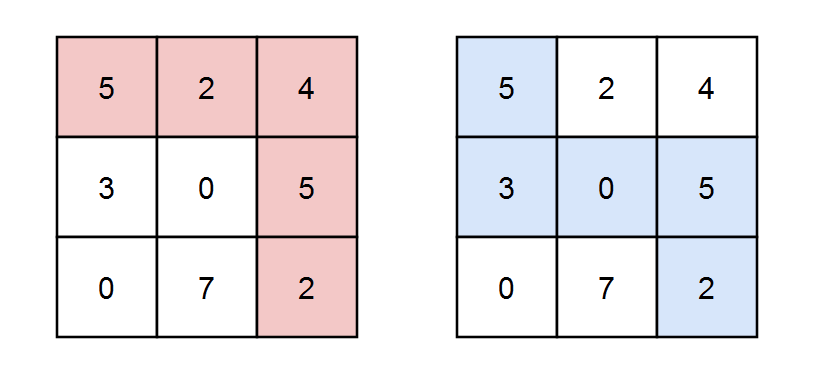
输入:grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
输出:2
解释:有两条路径满足路径上元素的和能被 k 整除。
第一条路径为上图中用红色标注的路径,和为 5 + 2 + 4 + 5 + 2 = 18 ,能被 3 整除。
第二条路径为上图中用蓝色标注的路径,和为 5 + 3 + 0 + 5 + 2 = 15 ,能被 3 整除。
示例 2:
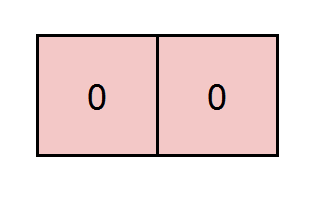
输入:grid = [[0,0]], k = 5
输出:1
解释:红色标注的路径和为 0 + 0 = 0 ,能被 5 整除。
示例 3:
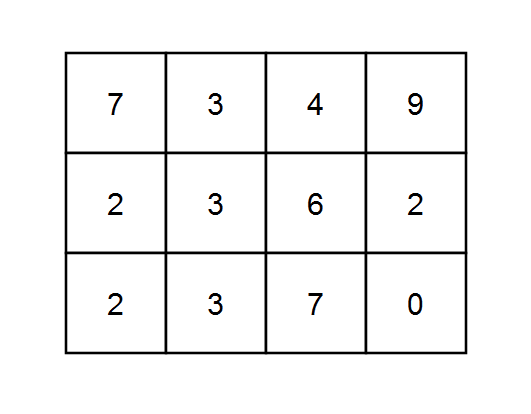
输入:grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1
输出:10
解释:每个数字都能被 1 整除,所以每一条路径的和都能被 k 整除。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 5 * 1041 <= m * n <= 5 * 1040 <= grid[i][j] <= 1001 <= k <= 50
解法
方法一:记忆化搜索
设计函数 dfs(i, j, s) 表示从 (i, j) 出发,初始路径和模 $k$ 的结果为 $s$ 的路径数目。
对于每个位置 $(i, j)$,我们可以选择向右或向下移动,因此有:
$$
dfs(i, j, s) = dfs(i + 1, j, (s + grid[i][j]) \bmod k) + dfs(i, j + 1, (s + grid[i][j]) \bmod k)
$$
答案为 dfs(0, 0, 0)。记忆化搜索即可。
时间复杂度 $O(m \times n \times k)$,空间复杂度 $O(m \times n \times k)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数,而 $k$ 为给定的整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution:
def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
@cache
def dfs(i, j, s):
if i < 0 or i >= m or j < 0 or j >= n:
return 0
s = (s + grid[i][j]) % k
if i == m - 1 and j == n - 1:
return int(s == 0)
ans = dfs(i + 1, j, s) + dfs(i, j + 1, s)
return ans % mod
m, n = len(grid), len(grid[0])
mod = 10**9 + 7
ans = dfs(0, 0, 0)
dfs.cache_clear()
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 | class Solution {
private int m;
private int n;
private int k;
private static final int MOD = (int) 1e9 + 7;
private int[][] grid;
private int[][][] f;
public int numberOfPaths(int[][] grid, int k) {
this.grid = grid;
this.k = k;
m = grid.length;
n = grid[0].length;
f = new int[m][n][k];
for (var a : f) {
for (var b : a) {
Arrays.fill(b, -1);
}
}
return dfs(0, 0, 0);
}
private int dfs(int i, int j, int s) {
if (i < 0 || i >= m || j < 0 || j >= n) {
return 0;
}
s = (s + grid[i][j]) % k;
if (f[i][j][s] != -1) {
return f[i][j][s];
}
if (i == m - 1 && j == n - 1) {
return s == 0 ? 1 : 0;
}
int ans = dfs(i + 1, j, s) + dfs(i, j + 1, s);
ans %= MOD;
f[i][j][s] = ans;
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution {
public:
int numberOfPaths(vector<vector<int>>& grid, int k) {
int m = grid.size(), n = grid[0].size();
int mod = 1e9 + 7;
vector<vector<vector<int>>> f(m, vector<vector<int>>(n, vector<int>(k, -1)));
function<int(int, int, int)> dfs;
dfs = [&](int i, int j, int s) {
if (i < 0 || i >= m || j < 0 || j >= n) return 0;
s = (s + grid[i][j]) % k;
if (i == m - 1 && j == n - 1) return s == 0 ? 1 : 0;
if (f[i][j][s] != -1) return f[i][j][s];
int ans = dfs(i + 1, j, s) + dfs(i, j + 1, s);
ans %= mod;
f[i][j][s] = ans;
return ans;
};
return dfs(0, 0, 0);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | func numberOfPaths(grid [][]int, k int) int {
m, n := len(grid), len(grid[0])
var mod int = 1e9 + 7
f := make([][][]int, m)
for i := range f {
f[i] = make([][]int, n)
for j := range f[i] {
f[i][j] = make([]int, k)
for x := 0; x < k; x++ {
f[i][j][x] = -1
}
}
}
var dfs func(i, j, s int) int
dfs = func(i, j, s int) int {
if i < 0 || i >= m || j < 0 || j >= n {
return 0
}
s = (s + grid[i][j]) % k
if i == m-1 && j == n-1 {
if s == 0 {
return 1
}
return 0
}
if f[i][j][s] != -1 {
return f[i][j][s]
}
ans := dfs(i+1, j, s) + dfs(i, j+1, s)
ans %= mod
f[i][j][s] = ans
return ans
}
return dfs(0, 0, 0)
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | function numberOfPaths(grid: number[][], k: number): number {
const MOD = 10 ** 9 + 7;
const m = grid.length,
n = grid[0].length;
let ans = Array.from({ length: m + 1 }, () =>
Array.from({ length: n + 1 }, () => new Array(k).fill(0)),
);
ans[0][1][0] = 1;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
for (let v = 0; v < k; v++) {
let key = (grid[i][j] + v) % k;
ans[i + 1][j + 1][key] =
(ans[i][j + 1][v] + ans[i + 1][j][v] + ans[i + 1][j + 1][key]) % MOD;
}
}
}
return ans[m][n][0];
}
|
方法二:动态规划
我们也可以使用动态规划求解。
定义状态 $dp[i][j][s]$ 表示从起点 $(0, 0)$ 出发,到达位置 $(i, j)$,路径和模 $k$ 等于 $s$ 的路径数目。
初始值 $dp[0][0][grid[0][0] \bmod k] = 1$,答案为 $dp[m - 1][n - 1][0]$。
我们可以得到状态转移方程:
$$
dp[i][j][s] = dp[i - 1][j][(s - grid[i][j])\bmod k] + dp[i][j - 1][(s - grid[i][j])\bmod k]
$$
时间复杂度 $O(m \times n \times k)$,空间复杂度 $O(m \times n \times k)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数,而 $k$ 为给定的整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | class Solution:
def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
m, n = len(grid), len(grid[0])
dp = [[[0] * k for _ in range(n)] for _ in range(m)]
dp[0][0][grid[0][0] % k] = 1
mod = 10**9 + 7
for i in range(m):
for j in range(n):
for s in range(k):
t = ((s - grid[i][j] % k) + k) % k
if i:
dp[i][j][s] += dp[i - 1][j][t]
if j:
dp[i][j][s] += dp[i][j - 1][t]
dp[i][j][s] %= mod
return dp[-1][-1][0]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | class Solution {
private static final int MOD = (int) 1e9 + 7;
public int numberOfPaths(int[][] grid, int k) {
int m = grid.length, n = grid[0].length;
int[][][] dp = new int[m][n][k];
dp[0][0][grid[0][0] % k] = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int s = 0; s < k; ++s) {
int t = ((s - grid[i][j] % k) + k) % k;
if (i > 0) {
dp[i][j][s] += dp[i - 1][j][t];
}
if (j > 0) {
dp[i][j][s] += dp[i][j - 1][t];
}
dp[i][j][s] %= MOD;
}
}
}
return dp[m - 1][n - 1][0];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution {
public:
const int mod = 1e9 + 7;
int numberOfPaths(vector<vector<int>>& grid, int k) {
int m = grid.size(), n = grid[0].size();
vector<vector<vector<int>>> dp(m, vector<vector<int>>(n, vector<int>(k)));
dp[0][0][grid[0][0] % k] = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int s = 0; s < k; ++s) {
int t = ((s - grid[i][j] % k) + k) % k;
if (i) dp[i][j][s] += dp[i - 1][j][t];
if (j) dp[i][j][s] += dp[i][j - 1][t];
dp[i][j][s] %= mod;
}
}
}
return dp[m - 1][n - 1][0];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | func numberOfPaths(grid [][]int, k int) int {
m, n := len(grid), len(grid[0])
var mod int = 1e9 + 7
dp := make([][][]int, m)
for i := range dp {
dp[i] = make([][]int, n)
for j := range dp[i] {
dp[i][j] = make([]int, k)
}
}
dp[0][0][grid[0][0]%k] = 1
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
for s := 0; s < k; s++ {
t := ((s - grid[i][j]%k) + k) % k
if i > 0 {
dp[i][j][s] += dp[i-1][j][t]
}
if j > 0 {
dp[i][j][s] += dp[i][j-1][t]
}
dp[i][j][s] %= mod
}
}
}
return dp[m-1][n-1][0]
}
|





