Skip to content

999. Available Captures for Rook

Description

You are given an 8 x 8 matrix representing a chessboard. There is exactly one white rook represented by 'R', some number of white bishops 'B', and some number of black pawns 'p'. Empty squares are represented by '.'.

A rook can move any number of squares horizontally or vertically (up, down, left, right) until it reaches another piece or the edge of the board. A rook is attacking a pawn if it can move to the pawn's square in one move.

Note: A rook cannot move through other pieces, such as bishops or pawns. This means a rook cannot attack a pawn if there is another piece blocking the path.

Return the number of pawns the white rook is attacking.

 

Example 1:

Input: board = [[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","R",".",".",".","p"],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]

Output: 3

Explanation:

In this example, the rook is attacking all the pawns.

Example 2:

Input: board = [[".",".",".",".",".",".","."],[".","p","p","p","p","p",".","."],[".","p","p","B","p","p",".","."],[".","p","B","R","B","p",".","."],[".","p","p","B","p","p",".","."],[".","p","p","p","p","p",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]

Output: 0

Explanation:

The bishops are blocking the rook from attacking any of the pawns.

Example 3:

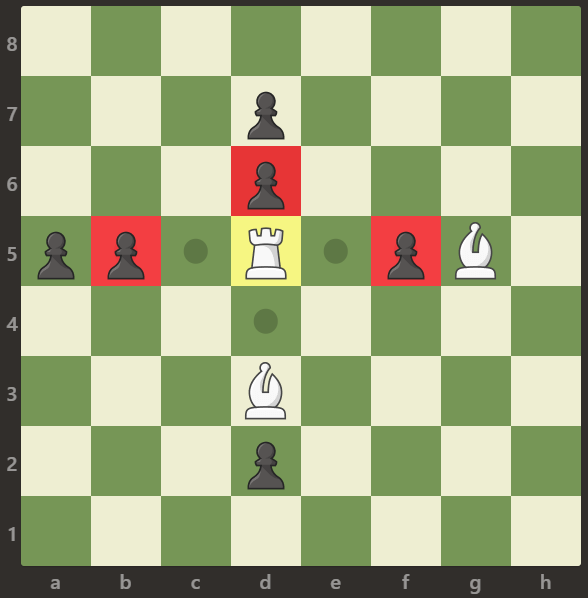
Input: board = [[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","p",".",".",".","."],["p","p",".","R",".","p","B","."],[".",".",".",".",".",".",".","."],[".",".",".","B",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."]]

Output: 3

Explanation:

The rook is attacking the pawns at positions b5, d6, and f5.

 

Constraints:

  • board.length == 8
  • board[i].length == 8
  • board[i][j] is either 'R', '.', 'B', or 'p'
  • There is exactly one cell with board[i][j] == 'R'

Solutions

Solution 1: Simulation

First, we traverse the chessboard to find the position of the rook $(x, y)$. Then, starting from $(x, y)$, we traverse in four directions: up, down, left, and right:

  • If we encounter a bishop or a boundary, we stop traversing in that direction.
  • If we encounter a pawn, we increment the answer by one, and then stop traversing in that direction.
  • Otherwise, we continue traversing.

After traversing in all four directions, we can get the answer.

The time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns of the chessboard, respectively. In this problem, $m = n = 8$. The space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution:
    def numRookCaptures(self, board: List[List[str]]) -> int:
        ans = 0
        dirs = (-1, 0, 1, 0, -1)
        for i in range(8):
            for j in range(8):
                if board[i][j] == "R":
                    for a, b in pairwise(dirs):
                        x, y = i, j
                        while 0 <= x + a < 8 and 0 <= y + b < 8:
                            x, y = x + a, y + b
                            if board[x][y] == "p":
                                ans += 1
                                break
                            if board[x][y] == "B":
                                break
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int numRookCaptures(char[][] board) {
        int ans = 0;
        int[] dirs = {-1, 0, 1, 0, -1};
        for (int i = 0; i < 8; ++i) {
            for (int j = 0; j < 8; ++j) {
                if (board[i][j] == 'R') {
                    for (int k = 0; k < 4; ++k) {
                        int x = i, y = j;
                        int a = dirs[k], b = dirs[k + 1];
                        while (x + a >= 0 && x + a < 8 && y + b >= 0 && y + b < 8
                            && board[x + a][y + b] != 'B') {
                            x += a;
                            y += b;
                            if (board[x][y] == 'p') {
                                ++ans;
                                break;
                            }
                        }
                    }
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int numRookCaptures(vector<vector<char>>& board) {
        int ans = 0;
        int dirs[5] = {-1, 0, 1, 0, -1};
        for (int i = 0; i < 8; ++i) {
            for (int j = 0; j < 8; ++j) {
                if (board[i][j] == 'R') {
                    for (int k = 0; k < 4; ++k) {
                        int x = i, y = j;
                        int a = dirs[k], b = dirs[k + 1];
                        while (x + a >= 0 && x + a < 8 && y + b >= 0 && y + b < 8 && board[x + a][y + b] != 'B') {
                            x += a;
                            y += b;
                            if (board[x][y] == 'p') {
                                ++ans;
                                break;
                            }
                        }
                    }
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
func numRookCaptures(board [][]byte) (ans int) {
    dirs := [5]int{-1, 0, 1, 0, -1}
    for i := 0; i < 8; i++ {
        for j := 0; j < 8; j++ {
            if board[i][j] == 'R' {
                for k := 0; k < 4; k++ {
                    x, y := i, j
                    a, b := dirs[k], dirs[k+1]
                    for x+a >= 0 && x+a < 8 && y+b >= 0 && y+b < 8 && board[x+a][y+b] != 'B' {
                        x, y = x+a, y+b
                        if board[x][y] == 'p' {
                            ans++
                            break
                        }
                    }
                }
            }
        }
    }
    return
}

Comments