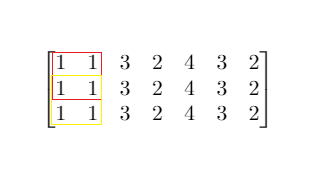Skip to content

1292. Maximum Side Length of a Square with Sum Less than or Equal to Threshold

Description

Given a m x n matrix mat and an integer threshold, return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.

 

Example 1:

Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

 

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 300
  • 0 <= mat[i][j] <= 104
  • 0 <= threshold <= 105

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
        def check(k: int) -> bool:
            for i in range(m - k + 1):
                for j in range(n - k + 1):
                    v = s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j]
                    if v <= threshold:
                        return True
            return False

        m, n = len(mat), len(mat[0])
        s = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(mat, 1):
            for j, x in enumerate(row, 1):
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + x
        l, r = 0, min(m, n)
        while l < r:
            mid = (l + r + 1) >> 1
            if check(mid):
                l = mid
            else:
                r = mid - 1
        return l

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    private int m;
    private int n;
    private int threshold;
    private int[][] s;

    public int maxSideLength(int[][] mat, int threshold) {
        m = mat.length;
        n = mat[0].length;
        this.threshold = threshold;
        s = new int[m + 1][n + 1];
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        int l = 0, r = Math.min(m, n);
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (check(mid)) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }

    private boolean check(int k) {
        for (int i = 0; i < m - k + 1; ++i) {
            for (int j = 0; j < n - k + 1; ++j) {
                if (s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j] <= threshold) {
                    return true;
                }
            }
        }
        return false;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int m = mat.size(), n = mat[0].size();
        int s[m + 1][n + 1];
        memset(s, 0, sizeof(s));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        auto check = [&](int k) {
            for (int i = 0; i < m - k + 1; ++i) {
                for (int j = 0; j < n - k + 1; ++j) {
                    if (s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j] <= threshold) {
                        return true;
                    }
                }
            }
            return false;
        };
        int l = 0, r = min(m, n);
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (check(mid)) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func maxSideLength(mat [][]int, threshold int) int {
    m, n := len(mat), len(mat[0])
    s := make([][]int, m+1)
    for i := range s {
        s[i] = make([]int, n+1)
    }
    for i := 1; i <= m; i++ {
        for j := 1; j <= n; j++ {
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + mat[i-1][j-1]
        }
    }
    check := func(k int) bool {
        for i := 0; i < m-k+1; i++ {
            for j := 0; j < n-k+1; j++ {
                if s[i+k][j+k]-s[i][j+k]-s[i+k][j]+s[i][j] <= threshold {
                    return true
                }
            }
        }
        return false
    }
    l, r := 0, min(m, n)
    for l < r {
        mid := (l + r + 1) >> 1
        if check(mid) {
            l = mid
        } else {
            r = mid - 1
        }
    }
    return l
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
function maxSideLength(mat: number[][], threshold: number): number {
    const m = mat.length;
    const n = mat[0].length;
    const s: number[][] = Array(m + 1)
        .fill(0)
        .map(() => Array(n + 1).fill(0));
    for (let i = 1; i <= m; ++i) {
        for (let j = 1; j <= n; ++j) {
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
        }
    }
    const check = (k: number): boolean => {
        for (let i = 0; i < m - k + 1; ++i) {
            for (let j = 0; j < n - k + 1; ++j) {
                if (s[i + k][j + k] - s[i + k][j] - s[i][j + k] + s[i][j] <= threshold) {
                    return true;
                }
            }
        }
        return false;
    };

    let l = 0;
    let r = Math.min(m, n);
    while (l < r) {
        const mid = (l + r + 1) >> 1;
        if (check(mid)) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }
    return l;
}

Comments