Skip to content

1594. Maximum Non Negative Product in a Matrix

Description

You are given a m x n matrix grid. Initially, you are located at the top-left corner (0, 0), and in each step, you can only move right or down in the matrix.

Among all possible paths starting from the top-left corner (0, 0) and ending in the bottom-right corner (m - 1, n - 1), find the path with the maximum non-negative product. The product of a path is the product of all integers in the grid cells visited along the path.

Return the maximum non-negative product modulo 109 + 7. If the maximum product is negative, return -1.

Notice that the modulo is performed after getting the maximum product.

 

Example 1:

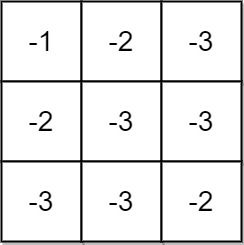
Input: grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]]
Output: -1
Explanation: It is not possible to get non-negative product in the path from (0, 0) to (2, 2), so return -1.

Example 2:

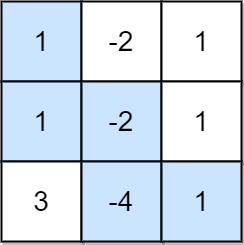
Input: grid = [[1,-2,1],[1,-2,1],[3,-4,1]]
Output: 8
Explanation: Maximum non-negative product is shown (1 * 1 * -2 * -4 * 1 = 8).

Example 3:

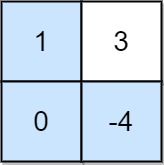
Input: grid = [[1,3],[0,-4]]
Output: 0
Explanation: Maximum non-negative product is shown (1 * 0 * -4 = 0).

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 15
  • -4 <= grid[i][j] <= 4

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def maxProductPath(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        mod = 10**9 + 7
        dp = [[[grid[0][0]] * 2 for _ in range(n)] for _ in range(m)]
        for i in range(1, m):
            dp[i][0] = [dp[i - 1][0][0] * grid[i][0]] * 2
        for j in range(1, n):
            dp[0][j] = [dp[0][j - 1][0] * grid[0][j]] * 2
        for i in range(1, m):
            for j in range(1, n):
                v = grid[i][j]
                if v >= 0:
                    dp[i][j][0] = min(dp[i - 1][j][0], dp[i][j - 1][0]) * v
                    dp[i][j][1] = max(dp[i - 1][j][1], dp[i][j - 1][1]) * v
                else:
                    dp[i][j][0] = max(dp[i - 1][j][1], dp[i][j - 1][1]) * v
                    dp[i][j][1] = min(dp[i - 1][j][0], dp[i][j - 1][0]) * v
        ans = dp[-1][-1][1]
        return -1 if ans < 0 else ans % mod

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    private static final int MOD = (int) 1e9 + 7;

    public int maxProductPath(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        long[][][] dp = new long[m][n][2];
        dp[0][0][0] = grid[0][0];
        dp[0][0][1] = grid[0][0];
        for (int i = 1; i < m; ++i) {
            dp[i][0][0] = dp[i - 1][0][0] * grid[i][0];
            dp[i][0][1] = dp[i - 1][0][1] * grid[i][0];
        }
        for (int j = 1; j < n; ++j) {
            dp[0][j][0] = dp[0][j - 1][0] * grid[0][j];
            dp[0][j][1] = dp[0][j - 1][1] * grid[0][j];
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                int v = grid[i][j];
                if (v >= 0) {
                    dp[i][j][0] = Math.min(dp[i - 1][j][0], dp[i][j - 1][0]) * v;
                    dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i][j - 1][1]) * v;
                } else {
                    dp[i][j][0] = Math.max(dp[i - 1][j][1], dp[i][j - 1][1]) * v;
                    dp[i][j][1] = Math.min(dp[i - 1][j][0], dp[i][j - 1][0]) * v;
                }
            }
        }
        long ans = dp[m - 1][n - 1][1];
        return ans < 0 ? -1 : (int) (ans % MOD);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
using ll = long long;
const int mod = 1e9 + 7;

class Solution {
public:
    int maxProductPath(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<vector<ll>>> dp(m, vector<vector<ll>>(n, vector<ll>(2, grid[0][0])));
        for (int i = 1; i < m; ++i) {
            dp[i][0][0] = dp[i - 1][0][0] * grid[i][0];
            dp[i][0][1] = dp[i - 1][0][1] * grid[i][0];
        }
        for (int j = 1; j < n; ++j) {
            dp[0][j][0] = dp[0][j - 1][0] * grid[0][j];
            dp[0][j][1] = dp[0][j - 1][1] * grid[0][j];
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                int v = grid[i][j];
                if (v >= 0) {
                    dp[i][j][0] = min(dp[i - 1][j][0], dp[i][j - 1][0]) * v;
                    dp[i][j][1] = max(dp[i - 1][j][1], dp[i][j - 1][1]) * v;
                } else {
                    dp[i][j][0] = max(dp[i - 1][j][1], dp[i][j - 1][1]) * v;
                    dp[i][j][1] = min(dp[i - 1][j][0], dp[i][j - 1][0]) * v;
                }
            }
        }
        ll ans = dp[m - 1][n - 1][1];
        return ans < 0 ? -1 : (int) (ans % mod);
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
func maxProductPath(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    dp := make([][][]int, m)
    for i := range dp {
        dp[i] = make([][]int, n)
        for j := range dp[i] {
            dp[i][j] = make([]int, 2)
        }
    }
    dp[0][0] = []int{grid[0][0], grid[0][0]}
    for i := 1; i < m; i++ {
        dp[i][0][0] = dp[i-1][0][0] * grid[i][0]
        dp[i][0][1] = dp[i-1][0][1] * grid[i][0]
    }
    for j := 1; j < n; j++ {
        dp[0][j][0] = dp[0][j-1][0] * grid[0][j]
        dp[0][j][1] = dp[0][j-1][1] * grid[0][j]
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n; j++ {
            v := grid[i][j]
            if v >= 0 {
                dp[i][j][0] = min(dp[i-1][j][0], dp[i][j-1][0]) * v
                dp[i][j][1] = max(dp[i-1][j][1], dp[i][j-1][1]) * v
            } else {
                dp[i][j][0] = max(dp[i-1][j][1], dp[i][j-1][1]) * v
                dp[i][j][1] = min(dp[i-1][j][0], dp[i][j-1][0]) * v
            }
        }
    }
    ans := dp[m-1][n-1][1]
    if ans < 0 {
        return -1
    }
    var mod int = 1e9 + 7
    return ans % mod
}

Comments