Skip to content

542. 01 Matrix

Description

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

 

Example 1:

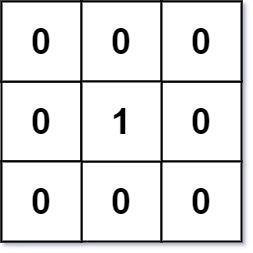
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

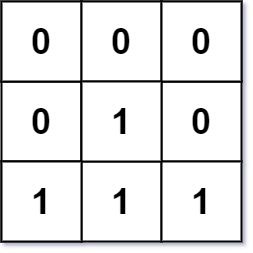
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

 

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 104
  • 1 <= m * n <= 104
  • mat[i][j] is either 0 or 1.
  • There is at least one 0 in mat.

Solutions

Solution 1: BFS

We create a matrix $\textit{ans}$ of the same size as $\textit{mat}$ and initialize all elements to $-1$.

Then, we traverse $\textit{mat}$, adding the coordinates $(i, j)$ of all $0$ elements to the queue $\textit{q}$, and setting $\textit{ans}[i][j]$ to $0$.

Next, we use Breadth-First Search (BFS), removing an element $(i, j)$ from the queue and traversing its four directions. If the element in that direction $(x, y)$ satisfies $0 \leq x < m$, $0 \leq y < n$ and $\textit{ans}[x][y] = -1$, then we set $\textit{ans}[x][y]$ to $\textit{ans}[i][j] + 1$ and add $(x, y)$ to the queue $\textit{q}$.

Finally, we return $\textit{ans}$.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the number of rows and columns in the matrix $\textit{mat}$, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        m, n = len(mat), len(mat[0])
        ans = [[-1] * n for _ in range(m)]
        q = deque()
        for i, row in enumerate(mat):
            for j, x in enumerate(row):
                if x == 0:
                    ans[i][j] = 0
                    q.append((i, j))
        dirs = (-1, 0, 1, 0, -1)
        while q:
            i, j = q.popleft()
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and ans[x][y] == -1:
                    ans[x][y] = ans[i][j] + 1
                    q.append((x, y))
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int[][] updateMatrix(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[][] ans = new int[m][n];
        for (int[] row : ans) {
            Arrays.fill(row, -1);
        }
        Deque<int[]> q = new ArrayDeque<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 0) {
                    q.offer(new int[] {i, j});
                    ans[i][j] = 0;
                }
            }
        }
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int i = p[0], j = p[1];
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1) {
                    ans[x][y] = ans[i][j] + 1;
                    q.offer(new int[] {x, y});
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> ans(m, vector<int>(n, -1));
        queue<pair<int, int>> q;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 0) {
                    ans[i][j] = 0;
                    q.emplace(i, j);
                }
            }
        }
        vector<int> dirs = {-1, 0, 1, 0, -1};
        while (!q.empty()) {
            auto p = q.front();
            q.pop();
            for (int i = 0; i < 4; ++i) {
                int x = p.first + dirs[i];
                int y = p.second + dirs[i + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1) {
                    ans[x][y] = ans[p.first][p.second] + 1;
                    q.emplace(x, y);
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
func updateMatrix(mat [][]int) [][]int {
    m, n := len(mat), len(mat[0])
    ans := make([][]int, m)
    for i := range ans {
        ans[i] = make([]int, n)
        for j := range ans[i] {
            ans[i][j] = -1
        }
    }
    type pair struct{ x, y int }
    var q []pair
    for i, row := range mat {
        for j, v := range row {
            if v == 0 {
                ans[i][j] = 0
                q = append(q, pair{i, j})
            }
        }
    }
    dirs := []int{-1, 0, 1, 0, -1}
    for len(q) > 0 {
        p := q[0]
        q = q[1:]
        for i := 0; i < 4; i++ {
            x, y := p.x+dirs[i], p.y+dirs[i+1]
            if x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1 {
                ans[x][y] = ans[p.x][p.y] + 1
                q = append(q, pair{x, y})
            }
        }
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function updateMatrix(mat: number[][]): number[][] {
    const [m, n] = [mat.length, mat[0].length];
    const ans: number[][] = Array.from({ length: m }, () => Array.from({ length: n }, () => -1));
    const q: [number, number][] = [];
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (mat[i][j] === 0) {
                q.push([i, j]);
                ans[i][j] = 0;
            }
        }
    }
    const dirs: number[] = [-1, 0, 1, 0, -1];
    for (const [i, j] of q) {
        for (let k = 0; k < 4; ++k) {
            const [x, y] = [i + dirs[k], j + dirs[k + 1]];
            if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] === -1) {
                ans[x][y] = ans[i][j] + 1;
                q.push([x, y]);
            }
        }
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
use std::collections::VecDeque;

impl Solution {
    pub fn update_matrix(mat: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let m = mat.len();
        let n = mat[0].len();
        let mut ans = vec![vec![-1; n]; m];
        let mut q = VecDeque::new();

        for i in 0..m {
            for j in 0..n {
                if mat[i][j] == 0 {
                    q.push_back((i, j));
                    ans[i][j] = 0;
                }
            }
        }

        let dirs = [-1, 0, 1, 0, -1];
        while let Some((i, j)) = q.pop_front() {
            for k in 0..4 {
                let x = i as isize + dirs[k];
                let y = j as isize + dirs[k + 1];
                if x >= 0 && x < m as isize && y >= 0 && y < n as isize {
                    let x = x as usize;
                    let y = y as usize;
                    if ans[x][y] == -1 {
                        ans[x][y] = ans[i][j] + 1;
                        q.push_back((x, y));
                    }
                }
            }
        }

        ans
    }
}

Comments