1901. Find a Peak Element II

Description

A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.

Given a 0-indexed m x n matrix mat where no two adjacent cells are equal, find any peak element mat[i][j] and return the length 2 array [i,j].

You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell.

You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time.

 

Example 1:

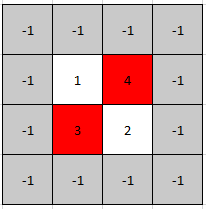
Input: mat = [[1,4],[3,2]]
Output: [0,1]
Explanation: Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.

Example 2:

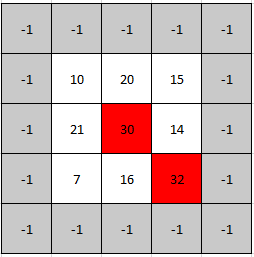
Input: mat = [[10,20,15],[21,30,14],[7,16,32]]
Output: [1,1]
Explanation: Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 500
• 1 <= mat[i][j] <= 105
• No two adjacent cells are equal.

Solutions

Solution 1: Binary Search

Let \(m\) and \(n\) be the number of rows and columns of the matrix, respectively.

The problem asks us to find a peak, and the time complexity should be \(O(m \times \log n)\) or \(O(n \times \log m)\). Therefore, we can consider using binary search.

We consider the maximum value of the \(i\)-th row, and denote its index as \(j\).

If \(mat[i][j] > mat[i + 1][j]\), then there must be a peak in the rows \([0,..i]\). We only need to find the maximum value in these rows. Similarly, if \(mat[i][j] < mat[i + 1][j]\), then there must be a peak in the rows \([i + 1,..m - 1]\). We only need to find the maximum value in these rows.

Why is the above method correct? We can prove it by contradiction.

If \(mat[i][j] > mat[i + 1][j]\), suppose there is no peak in the rows \([0,..i]\). Then \(mat[i][j]\) is not a peak. Since \(mat[i][j]\) is the maximum value of the \(i\)-th row, and \(mat[i][j] > mat[i + 1][j]\), then \(mat[i][j] < mat[i - 1][j]\). We continue to consider from the \((i - 1)\)-th row upwards, and the maximum value of each row is less than the maximum value of the previous row. When we traverse to \(i = 0\), since all elements in the matrix are positive integers, and the values of the cells around the matrix are \(-1\). Therefore, at the 0-th row, its maximum value is greater than all its adjacent elements, so the maximum value of the 0-th row is a peak, which contradicts the assumption. Therefore, there must be a peak in the rows \([0,..i]\).

For the case where \(mat[i][j] < mat[i + 1][j]\), we can prove in a similar way that there must be a peak in the rows \([i + 1,..m - 1]\).

Therefore, we can use binary search to find the peak.

We perform binary search on the rows of the matrix, initially with the search boundaries \(l = 0\), \(r = m - 1\). Each time, we find the middle row \(mid\) and find the index \(j\) of the maximum value of this row. If \(mat[mid][j] > mat[mid + 1][j]\), then we search for the peak in the rows \([0,..mid]\), i.e., update \(r = mid\). Otherwise, we search for the peak in the rows \([mid + 1,..m - 1]\), i.e., update \(l = mid + 1\). When \(l = r\), we find the position \([l, j_l]\) of the peak, where \(j_l\) is the index of the maximum value of the \(l\)-th row.

The time complexity is \(O(n \times \log m)\), where \(m\) and \(n\) are the number of rows and columns of the matrix, respectively. The time complexity of binary search is \(O(\log m)\), and each time we perform binary search, we need to traverse all elements of the \(mid\)-th row, with a time complexity of \(O(n)\). The space complexity is \(O(1)\).

Python3JavaC++GoTypeScriptRust

class Solution:
    def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
        l, r = 0, len(mat) - 1
        while l < r:
            mid = (l + r) >> 1
            j = mat[mid].index(max(mat[mid]))
            if mat[mid][j] > mat[mid + 1][j]:
                r = mid
            else:
                l = mid + 1
        return [l, mat[l].index(max(mat[l]))]

class Solution {
    public int[] findPeakGrid(int[][] mat) {
        int l = 0, r = mat.length - 1;
        int n = mat[0].length;
        while (l < r) {
            int mid = (l + r) >> 1;
            int j = maxPos(mat[mid]);
            if (mat[mid][j] > mat[mid + 1][j]) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return new int[] {l, maxPos(mat[l])};
    }

    private int maxPos(int[] arr) {
        int j = 0;
        for (int i = 1; i < arr.length; ++i) {
            if (arr[j] < arr[i]) {
                j = i;
            }
        }
        return j;
    }
}

class Solution {
public:
    vector<int> findPeakGrid(vector<vector<int>>& mat) {
        int l = 0, r = mat.size() - 1;
        while (l < r) {
            int mid = (l + r) >> 1;
            int j = distance(mat[mid].begin(), max_element(mat[mid].begin(), mat[mid].end()));
            if (mat[mid][j] > mat[mid + 1][j]) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        int j = distance(mat[l].begin(), max_element(mat[l].begin(), mat[l].end()));
        return {l, j};
    }
};

func findPeakGrid(mat [][]int) []int {
    maxPos := func(arr []int) int {
        j := 0
        for i := 1; i < len(arr); i++ {
            if arr[i] > arr[j] {
                j = i
            }
        }
        return j
    }
    l, r := 0, len(mat)-1
    for l < r {
        mid := (l + r) >> 1
        j := maxPos(mat[mid])
        if mat[mid][j] > mat[mid+1][j] {
            r = mid
        } else {
            l = mid + 1
        }
    }
    return []int{l, maxPos(mat[l])}
}

function findPeakGrid(mat: number[][]): number[] {
    let [l, r] = [0, mat.length - 1];
    while (l < r) {
        const mid = (l + r) >> 1;
        const j = mat[mid].indexOf(Math.max(...mat[mid]));
        if (mat[mid][j] > mat[mid + 1][j]) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    return [l, mat[l].indexOf(Math.max(...mat[l]))];
}

impl Solution {
    pub fn find_peak_grid(mat: Vec<Vec<i32>>) -> Vec<i32> {
        let mut l: usize = 0;
        let mut r: usize = mat.len() - 1;
        while l < r {
            let mid: usize = (l + r) >> 1;
            let j: usize = mat[mid]
                .iter()
                .position(|&x| x == *mat[mid].iter().max().unwrap())
                .unwrap();
            if mat[mid][j] > mat[mid + 1][j] {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        let j: usize = mat[l]
            .iter()
            .position(|&x| x == *mat[l].iter().max().unwrap())
            .unwrap();
        vec![l as i32, j as i32]
    }
}

Comments