Skip to content

782. Transform to Chessboard

Description

You are given an n x n binary grid board. In each move, you can swap any two rows with each other, or any two columns with each other.

Return the minimum number of moves to transform the board into a chessboard board. If the task is impossible, return -1.

A chessboard board is a board where no 0's and no 1's are 4-directionally adjacent.

 

Example 1:

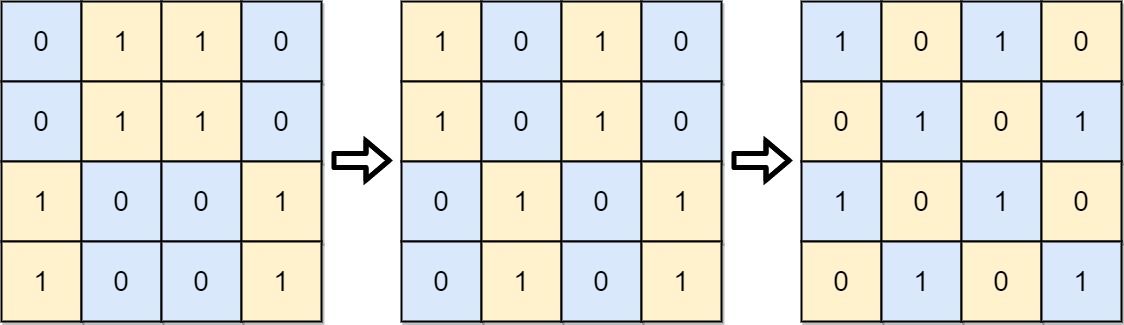
Input: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
Output: 2
Explanation: One potential sequence of moves is shown.
The first move swaps the first and second column.
The second move swaps the second and third row.

Example 2:

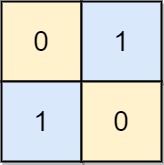
Input: board = [[0,1],[1,0]]
Output: 0
Explanation: Also note that the board with 0 in the top left corner, is also a valid chessboard.

Example 3:

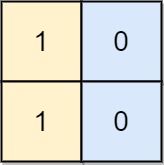
Input: board = [[1,0],[1,0]]
Output: -1
Explanation: No matter what sequence of moves you make, you cannot end with a valid chessboard.

 

Constraints:

  • n == board.length
  • n == board[i].length
  • 2 <= n <= 30
  • board[i][j] is either 0 or 1.

Solutions

Solution 1: Pattern Observation + State Compression

In a valid chessboard, there are exactly two types of "rows".

For example, if one row on the chessboard is "01010011", then any other row can only be "01010011" or "10101100". Columns also satisfy this property.

Additionally, each row and each column has half $0$s and half $1$s. Suppose the chessboard is $n \times n$:

  • If $n = 2 \times k$, then each row and each column has $k$ $1$s and $k$ $0$s.
  • If $n = 2 \times k + 1$, then each row has $k$ $1$s and $k + 1$ $0$s, or $k + 1$ $1$s and $k$ $0$s.

Based on the above conclusions, we can determine whether a chessboard is valid. If valid, we can calculate the minimum number of moves required.

If $n$ is even, there are two possible valid chessboards, where the first row is either "010101..." or "101010...". We calculate the minimum number of swaps required for these two possibilities and take the smaller value as the answer.

If $n$ is odd, there is only one possible valid chessboard. If the number of $0$s in the first row is greater than the number of $1$s, then the first row of the final chessboard must be "01010..."; otherwise, it must be "10101...". We calculate the number of swaps required and use it as the answer.

The time complexity is $O(n^2)$, where $n$ is the size of the chessboard. The space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution:
    def movesToChessboard(self, board: List[List[int]]) -> int:
        def f(mask, cnt):
            ones = mask.bit_count()
            if n & 1:
                if abs(n - 2 * ones) != 1 or abs(n - 2 * cnt) != 1:
                    return -1
                if ones == n // 2:
                    return n // 2 - (mask & 0xAAAAAAAA).bit_count()
                return (n + 1) // 2 - (mask & 0x55555555).bit_count()
            else:
                if ones != n // 2 or cnt != n // 2:
                    return -1
                cnt0 = n // 2 - (mask & 0xAAAAAAAA).bit_count()
                cnt1 = n // 2 - (mask & 0x55555555).bit_count()
                return min(cnt0, cnt1)

        n = len(board)
        mask = (1 << n) - 1
        rowMask = colMask = 0
        for i in range(n):
            rowMask |= board[0][i] << i
            colMask |= board[i][0] << i
        revRowMask = mask ^ rowMask
        revColMask = mask ^ colMask
        sameRow = sameCol = 0
        for i in range(n):
            curRowMask = curColMask = 0
            for j in range(n):
                curRowMask |= board[i][j] << j
                curColMask |= board[j][i] << j
            if curRowMask not in (rowMask, revRowMask) or curColMask not in (
                colMask,
                revColMask,
            ):
                return -1
            sameRow += curRowMask == rowMask
            sameCol += curColMask == colMask
        t1 = f(rowMask, sameRow)
        t2 = f(colMask, sameCol)
        return -1 if t1 == -1 or t2 == -1 else t1 + t2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Solution {
    private int n;

    public int movesToChessboard(int[][] board) {
        n = board.length;
        int mask = (1 << n) - 1;
        int rowMask = 0, colMask = 0;
        for (int i = 0; i < n; ++i) {
            rowMask |= board[0][i] << i;
            colMask |= board[i][0] << i;
        }
        int revRowMask = mask ^ rowMask;
        int revColMask = mask ^ colMask;
        int sameRow = 0, sameCol = 0;
        for (int i = 0; i < n; ++i) {
            int curRowMask = 0, curColMask = 0;
            for (int j = 0; j < n; ++j) {
                curRowMask |= board[i][j] << j;
                curColMask |= board[j][i] << j;
            }
            if (curRowMask != rowMask && curRowMask != revRowMask) {
                return -1;
            }
            if (curColMask != colMask && curColMask != revColMask) {
                return -1;
            }
            sameRow += curRowMask == rowMask ? 1 : 0;
            sameCol += curColMask == colMask ? 1 : 0;
        }
        int t1 = f(rowMask, sameRow);
        int t2 = f(colMask, sameCol);
        return t1 == -1 || t2 == -1 ? -1 : t1 + t2;
    }

    private int f(int mask, int cnt) {
        int ones = Integer.bitCount(mask);
        if (n % 2 == 1) {
            if (Math.abs(n - ones * 2) != 1 || Math.abs(n - cnt * 2) != 1) {
                return -1;
            }
            if (ones == n / 2) {
                return n / 2 - Integer.bitCount(mask & 0xAAAAAAAA);
            }
            return (n / 2 + 1) - Integer.bitCount(mask & 0x55555555);
        } else {
            if (ones != n / 2 || cnt != n / 2) {
                return -1;
            }
            int cnt0 = n / 2 - Integer.bitCount(mask & 0xAAAAAAAA);
            int cnt1 = n / 2 - Integer.bitCount(mask & 0x55555555);
            return Math.min(cnt0, cnt1);
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    int n;
    int movesToChessboard(vector<vector<int>>& board) {
        n = board.size();
        int mask = (1 << n) - 1;
        int rowMask = 0, colMask = 0;
        for (int i = 0; i < n; ++i) {
            rowMask |= board[0][i] << i;
            colMask |= board[i][0] << i;
        }
        int revRowMask = mask ^ rowMask;
        int revColMask = mask ^ colMask;
        int sameRow = 0, sameCol = 0;
        for (int i = 0; i < n; ++i) {
            int curRowMask = 0, curColMask = 0;
            for (int j = 0; j < n; ++j) {
                curRowMask |= board[i][j] << j;
                curColMask |= board[j][i] << j;
            }
            if (curRowMask != rowMask && curRowMask != revRowMask) return -1;
            if (curColMask != colMask && curColMask != revColMask) return -1;
            sameRow += curRowMask == rowMask;
            sameCol += curColMask == colMask;
        }
        int t1 = f(rowMask, sameRow);
        int t2 = f(colMask, sameCol);
        return t1 == -1 || t2 == -1 ? -1 : t1 + t2;
    }

    int f(int mask, int cnt) {
        int ones = __builtin_popcount(mask);
        if (n & 1) {
            if (abs(n - ones * 2) != 1 || abs(n - cnt * 2) != 1) return -1;
            if (ones == n / 2) return n / 2 - __builtin_popcount(mask & 0xAAAAAAAA);
            return (n + 1) / 2 - __builtin_popcount(mask & 0x55555555);
        } else {
            if (ones != n / 2 || cnt != n / 2) return -1;
            int cnt0 = (n / 2 - __builtin_popcount(mask & 0xAAAAAAAA));
            int cnt1 = (n / 2 - __builtin_popcount(mask & 0x55555555));
            return min(cnt0, cnt1);
        }
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
func movesToChessboard(board [][]int) int {
    n := len(board)
    mask := (1 << n) - 1
    rowMask, colMask := 0, 0
    for i := 0; i < n; i++ {
        rowMask |= board[0][i] << i
        colMask |= board[i][0] << i
    }
    revRowMask := mask ^ rowMask
    revColMask := mask ^ colMask
    sameRow, sameCol := 0, 0
    for i := 0; i < n; i++ {
        curRowMask, curColMask := 0, 0
        for j := 0; j < n; j++ {
            curRowMask |= board[i][j] << j
            curColMask |= board[j][i] << j
        }
        if curRowMask != rowMask && curRowMask != revRowMask {
            return -1
        }
        if curColMask != colMask && curColMask != revColMask {
            return -1
        }
        if curRowMask == rowMask {
            sameRow++
        }
        if curColMask == colMask {
            sameCol++
        }
    }
    f := func(mask, cnt int) int {
        ones := bits.OnesCount(uint(mask))
        if n%2 == 1 {
            if abs(n-ones*2) != 1 || abs(n-cnt*2) != 1 {
                return -1
            }
            if ones == n/2 {
                return n/2 - bits.OnesCount(uint(mask&0xAAAAAAAA))
            }
            return (n+1)/2 - bits.OnesCount(uint(mask&0x55555555))
        } else {
            if ones != n/2 || cnt != n/2 {
                return -1
            }
            cnt0 := n/2 - bits.OnesCount(uint(mask&0xAAAAAAAA))
            cnt1 := n/2 - bits.OnesCount(uint(mask&0x55555555))
            return min(cnt0, cnt1)
        }
    }
    t1 := f(rowMask, sameRow)
    t2 := f(colMask, sameCol)
    if t1 == -1 || t2 == -1 {
        return -1
    }
    return t1 + t2
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

Comments