Skip to content

847. Shortest Path Visiting All Nodes

Description

You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

 

Example 1:

Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

Example 2:

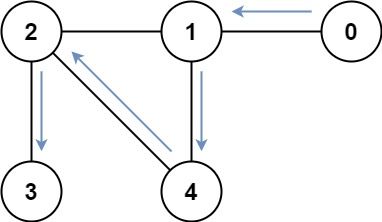
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]

 

Constraints:

  • n == graph.length
  • 1 <= n <= 12
  • 0 <= graph[i].length < n
  • graph[i] does not contain i.
  • If graph[a] contains b, then graph[b] contains a.
  • The input graph is always connected.

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)
        q = deque()
        vis = set()
        for i in range(n):
            q.append((i, 1 << i))
            vis.add((i, 1 << i))
        ans = 0
        while 1:
            for _ in range(len(q)):
                i, st = q.popleft()
                if st == (1 << n) - 1:
                    return ans
                for j in graph[i]:
                    nst = st | 1 << j
                    if (j, nst) not in vis:
                        vis.add((j, nst))
                        q.append((j, nst))
            ans += 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int shortestPathLength(int[][] graph) {
        int n = graph.length;
        Deque<int[]> q = new ArrayDeque<>();
        boolean[][] vis = new boolean[n][1 << n];
        for (int i = 0; i < n; ++i) {
            q.offer(new int[] {i, 1 << i});
            vis[i][1 << i] = true;
        }
        for (int ans = 0;; ++ans) {
            for (int k = q.size(); k > 0; --k) {
                var p = q.poll();
                int i = p[0], st = p[1];
                if (st == (1 << n) - 1) {
                    return ans;
                }
                for (int j : graph[i]) {
                    int nst = st | 1 << j;
                    if (!vis[j][nst]) {
                        vis[j][nst] = true;
                        q.offer(new int[] {j, nst});
                    }
                }
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int shortestPathLength(vector<vector<int>>& graph) {
        int n = graph.size();
        queue<pair<int, int>> q;
        bool vis[n][1 << n];
        memset(vis, false, sizeof(vis));
        for (int i = 0; i < n; ++i) {
            q.emplace(i, 1 << i);
            vis[i][1 << i] = true;
        }
        for (int ans = 0;; ++ans) {
            for (int k = q.size(); k; --k) {
                auto [i, st] = q.front();
                q.pop();
                if (st == (1 << n) - 1) {
                    return ans;
                }
                for (int j : graph[i]) {
                    int nst = st | 1 << j;
                    if (!vis[j][nst]) {
                        vis[j][nst] = true;
                        q.emplace(j, nst);
                    }
                }
            }
        }
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func shortestPathLength(graph [][]int) int {
    n := len(graph)
    q := [][2]int{}
    vis := make([][]bool, n)
    for i := range vis {
        vis[i] = make([]bool, 1<<n)
        vis[i][1<<i] = true
        q = append(q, [2]int{i, 1 << i})
    }
    for ans := 0; ; ans++ {
        for k := len(q); k > 0; k-- {
            p := q[0]
            q = q[1:]
            i, st := p[0], p[1]
            if st == (1<<n)-1 {
                return ans
            }
            for _, j := range graph[i] {
                nst := st | 1<<j
                if !vis[j][nst] {
                    vis[j][nst] = true
                    q = append(q, [2]int{j, nst})
                }
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function shortestPathLength(graph: number[][]): number {
    const n = graph.length;
    const q: number[][] = [];
    const vis: boolean[][] = new Array(n).fill(false).map(() => new Array(1 << n).fill(false));
    for (let i = 0; i < n; ++i) {
        q.push([i, 1 << i]);
        vis[i][1 << i] = true;
    }
    for (let ans = 0; ; ++ans) {
        for (let k = q.length; k; --k) {
            const [i, st] = q.shift()!;
            if (st === (1 << n) - 1) {
                return ans;
            }
            for (const j of graph[i]) {
                const nst = st | (1 << j);
                if (!vis[j][nst]) {
                    vis[j][nst] = true;
                    q.push([j, nst]);
                }
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
use std::collections::VecDeque;

impl Solution {
    #[allow(dead_code)]
    pub fn shortest_path_length(graph: Vec<Vec<i32>>) -> i32 {
        let n = graph.len();
        let mut vis = vec![vec![false; 1 << n]; n];
        let mut q = VecDeque::new();

        // Initialize the queue
        for i in 0..n {
            q.push_back(((i, 1 << i), 0));
            vis[i][1 << i] = true;
        }

        // Begin BFS
        while !q.is_empty() {
            let ((i, st), count) = q.pop_front().unwrap();
            if st == (1 << n) - 1 {
                return count;
            }
            // If the path has not been visited
            for j in &graph[i] {
                let nst = st | (1 << *j);
                if !vis[*j as usize][nst] {
                    q.push_back(((*j as usize, nst), count + 1));
                    vis[*j as usize][nst] = true;
                }
            }
        }

        -1
    }
}

Solution 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)

        def f(state):
            return sum(((state >> i) & 1) == 0 for i in range(n))

        q = []
        dist = [[inf] * (1 << n) for _ in range(n)]
        for i in range(n):
            heappush(q, (f(1 << i), i, 1 << i))
            dist[i][1 << i] = 0
        while q:
            _, u, state = heappop(q)
            if state == (1 << n) - 1:
                return dist[u][state]
            for v in graph[u]:
                nxt = state | (1 << v)
                if dist[v][nxt] > dist[u][state] + 1:
                    dist[v][nxt] = dist[u][state] + 1
                    heappush(q, (dist[v][nxt] + f(nxt), v, nxt))
        return 0

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    private int n;

    public int shortestPathLength(int[][] graph) {
        n = graph.length;
        int[][] dist = new int[n][1 << n];
        for (int i = 0; i < n; ++i) {
            Arrays.fill(dist[i], Integer.MAX_VALUE);
        }
        PriorityQueue<int[]> q = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        for (int i = 0; i < n; ++i) {
            q.offer(new int[] {f(1 << i), i, 1 << i});
            dist[i][1 << i] = 0;
        }
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int u = p[1], state = p[2];
            if (state == (1 << n) - 1) {
                return dist[u][state];
            }
            for (int v : graph[u]) {
                int nxt = state | (1 << v);
                if (dist[v][nxt] > dist[u][state] + 1) {
                    dist[v][nxt] = dist[u][state] + 1;
                    q.offer(new int[] {dist[v][nxt] + f(nxt), v, nxt});
                }
            }
        }
        return 0;
    }

    private int f(int state) {
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            if (((state >> i) & 1) == 0) {
                ++ans;
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    int n;

    int shortestPathLength(vector<vector<int>>& graph) {
        n = graph.size();
        priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> q;
        vector<vector<int>> dist(n, vector<int>(1 << n, INT_MAX));
        for (int i = 0; i < n; ++i) {
            q.push({f(1 << i), i, 1 << i});
            dist[i][1 << i] = 0;
        }
        while (!q.empty()) {
            auto [_, u, state] = q.top();
            q.pop();
            if (state == (1 << n) - 1) return dist[u][state];
            for (int v : graph[u]) {
                int nxt = state | (1 << v);
                if (dist[v][nxt] > dist[u][state] + 1) {
                    dist[v][nxt] = dist[u][state] + 1;
                    q.push({dist[v][nxt] + f(nxt), v, nxt});
                }
            }
        }
        return 0;
    }

    int f(int state) {
        int ans = 0;
        for (int i = 0; i < n; ++i)
            if (((state >> i) & 1) == 0)
                ++ans;
        return ans;
    }
};

Comments