Bit Manipulation
Array
Dynamic Programming
Bitmask
Description
You are given integers height and width which specify the dimensions of a brick wall you are building. You are also given a 0-indexed array of unique integers bricks, where the ith brick has a height of 1 and a width of bricks[i]. You have an infinite supply of each type of brick and bricks may not be rotated.
Each row in the wall must be exactly width units long. For the wall to be sturdy , adjacent rows in the wall should not join bricks at the same location, except at the ends of the wall.
Return the number of ways to build a sturdy wall. Since the answer may be very large, return it modulo 109 + 7.
Example 1:
Input: height = 2, width = 3, bricks = [1,2]
Output: 2
Explanation:
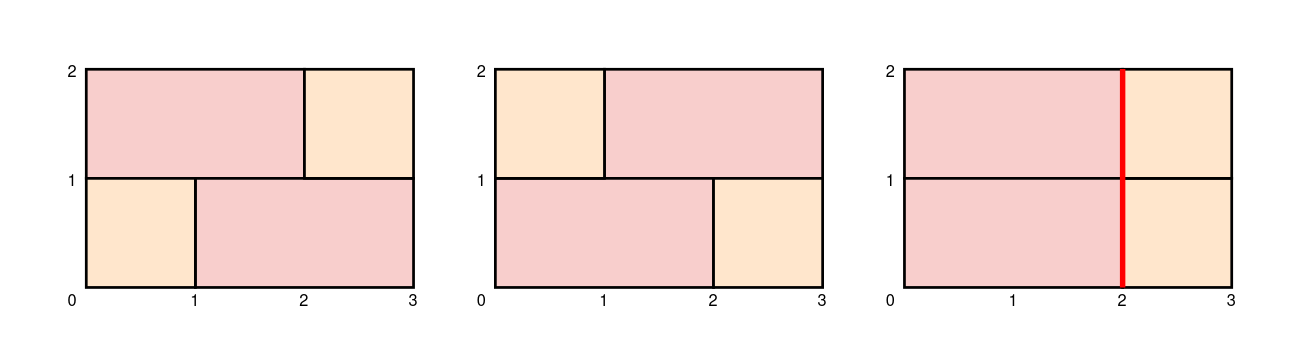
The first two walls in the diagram show the only two ways to build a sturdy brick wall.
Note that the third wall in the diagram is not sturdy because adjacent rows join bricks 2 units from the left.
Example 2:
Input: height = 1, width = 1, bricks = [5]
Output: 0
Explanation:
There are no ways to build a sturdy wall because the only type of brick we have is longer than the width of the wall.
Constraints:
1 <= height <= 1001 <= width <= 101 <= bricks.length <= 101 <= bricks[i] <= 10All the values of bricks are unique .
Solutions
Solution 1
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 class Solution :
def buildWall ( self , height : int , width : int , bricks : List [ int ]) -> int :
def dfs ( v ):
if v > width :
return
if v == width :
s . append ( t [:])
return
for x in bricks :
t . append ( x )
dfs ( v + x )
t . pop ()
def check ( a , b ):
s1 , s2 = a [ 0 ], b [ 0 ]
i = j = 1
while i < len ( a ) and j < len ( b ):
if s1 == s2 :
return False
if s1 < s2 :
s1 += a [ i ]
i += 1
else :
s2 += b [ j ]
j += 1
return True
mod = 10 ** 9 + 7
s = []
t = []
dfs ( 0 )
g = defaultdict ( list )
n = len ( s )
for i in range ( n ):
if check ( s [ i ], s [ i ]):
g [ i ] . append ( i )
for j in range ( i + 1 , n ):
if check ( s [ i ], s [ j ]):
g [ i ] . append ( j )
g [ j ] . append ( i )
dp = [[ 0 ] * n for _ in range ( height )]
for j in range ( n ):
dp [ 0 ][ j ] = 1
for i in range ( 1 , height ):
for j in range ( n ):
for k in g [ j ]:
dp [ i ][ j ] += dp [ i - 1 ][ k ]
dp [ i ][ j ] %= mod
return sum ( dp [ - 1 ]) % mod
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75 class Solution {
private List < List < Integer >> res = new ArrayList <> ();
private List < Integer > t = new ArrayList <> ();
private static final int MOD = ( int ) 1e9 + 7 ;
private int width ;
private int [] bricks ;
public int buildWall ( int height , int width , int [] bricks ) {
this . width = width ;
this . bricks = bricks ;
dfs ( 0 );
int n = res . size ();
List < Integer >[] g = new List [ n ] ;
Arrays . setAll ( g , k -> new ArrayList <> ());
for ( int i = 0 ; i < n ; ++ i ) {
if ( check ( res . get ( i ), res . get ( i ))) {
g [ i ] . add ( i );
}
for ( int j = i + 1 ; j < n ; ++ j ) {
if ( check ( res . get ( i ), res . get ( j ))) {
g [ i ] . add ( j );
g [ j ] . add ( i );
}
}
}
int [][] dp = new int [ height ][ n ] ;
for ( int j = 0 ; j < n ; ++ j ) {
dp [ 0 ][ j ] = 1 ;
}
for ( int i = 1 ; i < height ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
for ( int k : g [ j ] ) {
dp [ i ][ j ] = ( dp [ i ][ j ] + dp [ i - 1 ][ k ] ) % MOD ;
}
}
}
int ans = 0 ;
for ( int j = 0 ; j < n ; ++ j ) {
ans = ( ans + dp [ height - 1 ][ j ] ) % MOD ;
}
return ans ;
}
private boolean check ( List < Integer > a , List < Integer > b ) {
int s1 = a . get ( 0 );
int s2 = b . get ( 0 );
int i = 1 , j = 1 ;
while ( i < a . size () && j < b . size ()) {
if ( s1 == s2 ) {
return false ;
}
if ( s1 < s2 ) {
s1 += a . get ( i ++ );
} else {
s2 += b . get ( j ++ );
}
}
return true ;
}
private void dfs ( int v ) {
if ( v > width ) {
return ;
}
if ( v == width ) {
res . add ( new ArrayList <> ( t ));
return ;
}
for ( int x : bricks ) {
t . add ( x );
dfs ( v + x );
t . remove ( t . size () - 1 );
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70 class Solution {
public :
vector < int > bricks ;
int width ;
int mod = 1e9 + 7 ;
vector < vector < int >> res ;
vector < int > t ;
int buildWall ( int height , int width , vector < int >& bricks ) {
this -> width = width ;
this -> bricks = bricks ;
dfs ( 0 );
t . resize ( 0 );
int n = res . size ();
vector < vector < int >> g ( n );
for ( int i = 0 ; i < n ; ++ i ) {
if ( check ( res [ i ], res [ i ])) {
g [ i ]. push_back ( i );
}
for ( int j = i + 1 ; j < n ; ++ j ) {
if ( check ( res [ i ], res [ j ])) {
g [ i ]. push_back ( j );
g [ j ]. push_back ( i );
}
}
}
vector < vector < int >> dp ( height , vector < int > ( n ));
for ( int j = 0 ; j < n ; ++ j ) dp [ 0 ][ j ] = 1 ;
for ( int i = 1 ; i < height ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
for ( int k : g [ j ]) {
dp [ i ][ j ] += dp [ i - 1 ][ k ];
dp [ i ][ j ] %= mod ;
}
}
}
int ans = 0 ;
for ( int j = 0 ; j < n ; ++ j ) {
ans += dp [ height - 1 ][ j ];
ans %= mod ;
}
return ans ;
}
bool check ( vector < int >& a , vector < int >& b ) {
int s1 = a [ 0 ], s2 = b [ 0 ];
int i = 1 , j = 1 ;
while ( i < a . size () && j < b . size ()) {
if ( s1 == s2 ) return false ;
if ( s1 < s2 )
s1 += a [ i ++ ];
else
s2 += b [ j ++ ];
}
return true ;
}
void dfs ( int v ) {
if ( v > width ) return ;
if ( v == width ) {
res . push_back ( t );
return ;
}
for ( int x : bricks ) {
t . push_back ( x );
dfs ( v + x );
t . pop_back ();
}
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72 func buildWall ( height int , width int , bricks [] int ) int {
mod := int ( 1e9 ) + 7
res := [][] int {}
t := [] int {}
var dfs func ( int )
dfs = func ( v int ) {
if v > width {
return
}
if v == width {
res = append ( res , slices . Clone ( t ))
return
}
for _ , x := range bricks {
t = append ( t , x )
dfs ( v + x )
t = t [: len ( t ) - 1 ]
}
}
check := func ( a , b [] int ) bool {
s1 , s2 := a [ 0 ], b [ 0 ]
i , j := 1 , 1
for i < len ( a ) && j < len ( b ) {
if s1 == s2 {
return false
}
if s1 < s2 {
s1 += a [ i ]
i ++
} else {
s2 += b [ j ]
j ++
}
}
return true
}
dfs ( 0 )
n := len ( res )
g := make ([][] int , n )
for i := 0 ; i < n ; i ++ {
if check ( res [ i ], res [ i ]) {
g [ i ] = append ( g [ i ], i )
}
for j := i + 1 ; j < n ; j ++ {
if check ( res [ i ], res [ j ]) {
g [ i ] = append ( g [ i ], j )
g [ j ] = append ( g [ j ], i )
}
}
}
dp := make ([][] int , height )
for i := range dp {
dp [ i ] = make ([] int , n )
}
for j := 0 ; j < n ; j ++ {
dp [ 0 ][ j ] = 1
}
for i := 1 ; i < height ; i ++ {
for j := 0 ; j < n ; j ++ {
for _ , k := range g [ j ] {
dp [ i ][ j ] += dp [ i - 1 ][ k ]
dp [ i ][ j ] %= mod
}
}
}
ans := 0
for j := 0 ; j < n ; j ++ {
ans += dp [ height - 1 ][ j ]
ans %= mod
}
return ans
}
GitHub