Tree
Depth-First Search
Binary Search Tree
Binary Tree
Description
Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer .
Return the root of the trimmed binary search tree . Note that the root may change depending on the given bounds.
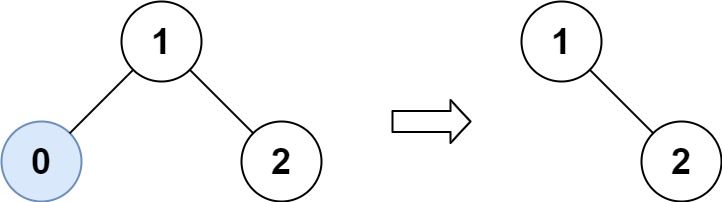
Example 1:
Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]
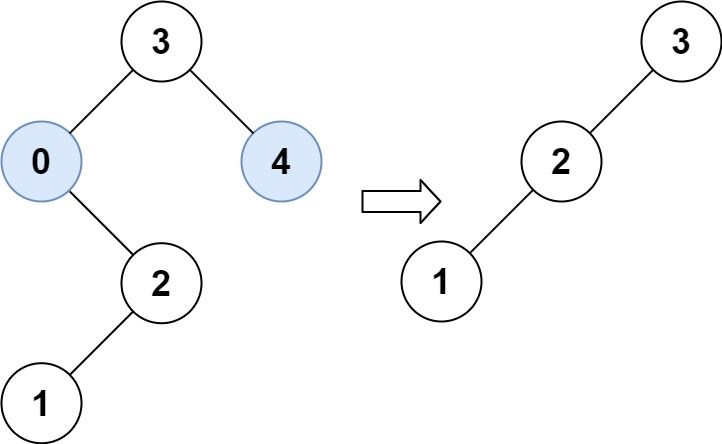
Example 2:
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]
Constraints:
The number of nodes in the tree is in the range [1, 104 ].
0 <= Node.val <= 104 The value of each node in the tree is unique .
root is guaranteed to be a valid binary search tree.0 <= low <= high <= 104
Solutions
Solution 1
Python3 Java C++ Go TypeScript Rust JavaScript C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def trimBST (
self , root : Optional [ TreeNode ], low : int , high : int
) -> Optional [ TreeNode ]:
def dfs ( root ):
if root is None :
return root
if root . val > high :
return dfs ( root . left )
if root . val < low :
return dfs ( root . right )
root . left = dfs ( root . left )
root . right = dfs ( root . right )
return root
return dfs ( root )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode trimBST ( TreeNode root , int low , int high ) {
if ( root == null ) {
return root ;
}
if ( root . val > high ) {
return trimBST ( root . left , low , high );
}
if ( root . val < low ) {
return trimBST ( root . right , low , high );
}
root . left = trimBST ( root . left , low , high );
root . right = trimBST ( root . right , low , high );
return root ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
TreeNode * trimBST ( TreeNode * root , int low , int high ) {
if ( ! root ) return root ;
if ( root -> val > high ) return trimBST ( root -> left , low , high );
if ( root -> val < low ) return trimBST ( root -> right , low , high );
root -> left = trimBST ( root -> left , low , high );
root -> right = trimBST ( root -> right , low , high );
return root ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func trimBST ( root * TreeNode , low int , high int ) * TreeNode {
if root == nil {
return root
}
if root . Val > high {
return trimBST ( root . Left , low , high )
}
if root . Val < low {
return trimBST ( root . Right , low , high )
}
root . Left = trimBST ( root . Left , low , high )
root . Right = trimBST ( root . Right , low , high )
return root
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function trimBST ( root : TreeNode | null , low : number , high : number ) : TreeNode | null {
const dfs = ( root : TreeNode | null ) => {
if ( root == null ) {
return root ;
}
const { val , left , right } = root ;
if ( val < low || val > high ) {
return dfs ( left ) || dfs ( right );
}
root . left = dfs ( left );
root . right = dfs ( right );
return root ;
};
return dfs ( root );
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std :: rc :: Rc ;
use std :: cell :: RefCell ;
impl Solution {
pub fn trim_bst (
mut root : Option < Rc < RefCell < TreeNode >>> ,
low : i32 ,
high : i32
) -> Option < Rc < RefCell < TreeNode >>> {
if root . is_none () {
return root ;
}
{
let mut node = root . as_mut (). unwrap (). borrow_mut ();
if node . val < low {
return Self :: trim_bst ( node . right . take (), low , high );
}
if node . val > high {
return Self :: trim_bst ( node . left . take (), low , high );
}
node . left = Self :: trim_bst ( node . left . take (), low , high );
node . right = Self :: trim_bst ( node . right . take (), low , high );
}
root
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 /**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} low
* @param {number} high
* @return {TreeNode}
*/
var trimBST = function ( root , low , high ) {
function dfs ( root ) {
if ( ! root ) {
return root ;
}
if ( root . val < low ) {
return dfs ( root . right );
}
if ( root . val > high ) {
return dfs ( root . left );
}
root . left = dfs ( root . left );
root . right = dfs ( root . right );
return root ;
}
return dfs ( root );
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
struct TreeNode * trimBST ( struct TreeNode * root , int low , int high ) {
if ( ! root ) {
return root ;
}
if ( root -> val < low ) {
return trimBST ( root -> right , low , high );
}
if ( root -> val > high ) {
return trimBST ( root -> left , low , high );
}
root -> left = trimBST ( root -> left , low , high );
root -> right = trimBST ( root -> right , low , high );
return root ;
}
Solution 2
Python3 Java C++ Go JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def trimBST (
self , root : Optional [ TreeNode ], low : int , high : int
) -> Optional [ TreeNode ]:
while root and ( root . val < low or root . val > high ):
root = root . left if root . val > high else root . right
if root is None :
return None
node = root
while node . left :
if node . left . val < low :
node . left = node . left . right
else :
node = node . left
node = root
while node . right :
if node . right . val > high :
node . right = node . right . left
else :
node = node . right
return root
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode trimBST ( TreeNode root , int low , int high ) {
while ( root != null && ( root . val < low || root . val > high )) {
root = root . val < low ? root . right : root . left ;
}
if ( root == null ) {
return null ;
}
TreeNode node = root ;
while ( node . left != null ) {
if ( node . left . val < low ) {
node . left = node . left . right ;
} else {
node = node . left ;
}
}
node = root ;
while ( node . right != null ) {
if ( node . right . val > high ) {
node . right = node . right . left ;
} else {
node = node . right ;
}
}
return root ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
TreeNode * trimBST ( TreeNode * root , int low , int high ) {
while ( root && ( root -> val < low || root -> val > high )) {
root = root -> val < low ? root -> right : root -> left ;
}
if ( ! root ) {
return root ;
}
TreeNode * node = root ;
while ( node -> left ) {
if ( node -> left -> val < low ) {
node -> left = node -> left -> right ;
} else {
node = node -> left ;
}
}
node = root ;
while ( node -> right ) {
if ( node -> right -> val > high ) {
node -> right = node -> right -> left ;
} else {
node = node -> right ;
}
}
return root ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func trimBST ( root * TreeNode , low int , high int ) * TreeNode {
for root != nil && ( root . Val < low || root . Val > high ) {
if root . Val < low {
root = root . Right
} else {
root = root . Left
}
}
if root == nil {
return nil
}
node := root
for node . Left != nil {
if node . Left . Val < low {
node . Left = node . Left . Right
} else {
node = node . Left
}
}
node = root
for node . Right != nil {
if node . Right . Val > high {
node . Right = node . Right . Left
} else {
node = node . Right
}
}
return root
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 /**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} low
* @param {number} high
* @return {TreeNode}
*/
var trimBST = function ( root , low , high ) {
while ( root && ( root . val < low || root . val > high )) {
root = root . val < low ? root . right : root . left ;
}
if ( ! root ) {
return root ;
}
let node = root ;
while ( node . left ) {
if ( node . left . val < low ) {
node . left = node . left . right ;
} else {
node = node . left ;
}
}
node = root ;
while ( node . right ) {
if ( node . right . val > high ) {
node . right = node . right . left ;
} else {
node = node . right ;
}
}
return root ;
};