Skip to content

2445. Number of Nodes With Value One πŸ”’

Description

There is an undirected connected tree with n nodes labeled from 1 to n and n - 1 edges. You are given the integer n. The parent node of a node with a label v is the node with the label floor (v / 2). The root of the tree is the node with the label 1.

  • For example, if n = 7, then the node with the label 3 has the node with the label floor(3 / 2) = 1 as its parent, and the node with the label 7 has the node with the label floor(7 / 2) = 3 as its parent.

You are also given an integer array queries. Initially, every node has a value 0 on it. For each query queries[i], you should flip all values in the subtree of the node with the label queries[i].

Return the total number of nodes with the value 1 after processing all the queries.

Note that:

  • Flipping the value of a node means that the node with the value 0 becomes 1 and vice versa.
  • floor(x) is equivalent to rounding x down to the nearest integer.

 

Example 1:

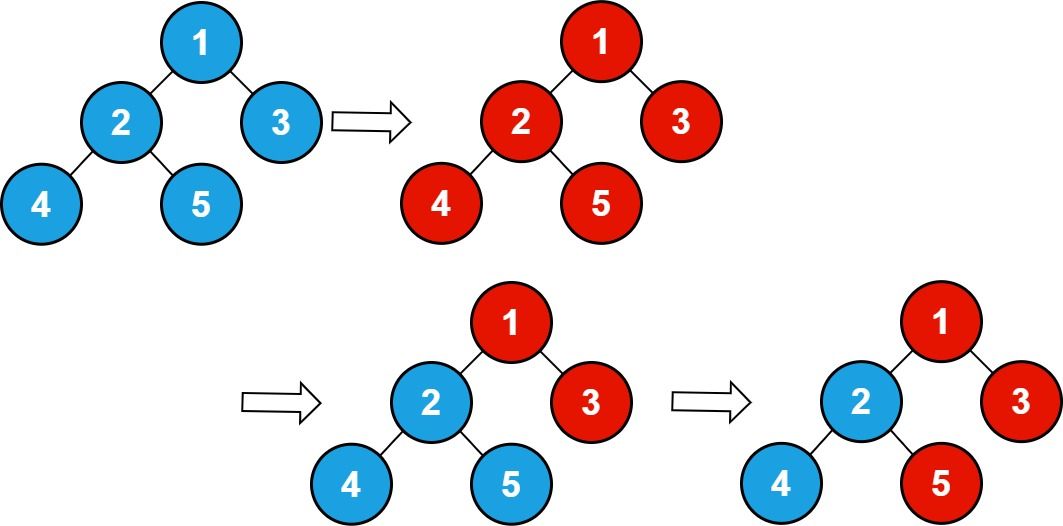
Input: n = 5 , queries = [1,2,5]
Output: 3
Explanation: The diagram above shows the tree structure and its status after performing the queries. The blue node represents the value 0, and the red node represents the value 1.
After processing the queries, there are three red nodes (nodes with value 1): 1, 3, and 5.

Example 2:

Input: n = 3, queries = [2,3,3]
Output: 1
Explanation: The diagram above shows the tree structure and its status after performing the queries. The blue node represents the value 0, and the red node represents the value 1.
After processing the queries, there are one red node (node with value 1): 2.

 

Constraints:

  • 1 <= n <= 105
  • 1 <= queries.length <= 105
  • 1 <= queries[i] <= n

Solutions

Solution 1: Simulation

According to the problem description, we can simulate the process of each query, that is, reverse the values of the query node and its subtree nodes. Finally, count the number of nodes with a value of 1.

There is an optimization point here. If a node and its corresponding subtree have been queried an even number of times, the node value will not change. Therefore, we can record the number of queries for each node, and only reverse the nodes and their subtrees that have been queried an odd number of times.

The time complexity is $O(n \times \log n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution:
    def numberOfNodes(self, n: int, queries: List[int]) -> int:
        def dfs(i):
            if i > n:
                return
            tree[i] ^= 1
            dfs(i << 1)
            dfs(i << 1 | 1)

        tree = [0] * (n + 1)
        cnt = Counter(queries)
        for i, v in cnt.items():
            if v & 1:
                dfs(i)
        return sum(tree)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    private int[] tree;

    public int numberOfNodes(int n, int[] queries) {
        tree = new int[n + 1];
        int[] cnt = new int[n + 1];
        for (int v : queries) {
            ++cnt[v];
        }
        for (int i = 0; i < n + 1; ++i) {
            if (cnt[i] % 2 == 1) {
                dfs(i);
            }
        }
        int ans = 0;
        for (int i = 0; i < n + 1; ++i) {
            ans += tree[i];
        }
        return ans;
    }

    private void dfs(int i) {
        if (i >= tree.length) {
            return;
        }
        tree[i] ^= 1;
        dfs(i << 1);
        dfs(i << 1 | 1);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int numberOfNodes(int n, vector<int>& queries) {
        vector<int> tree(n + 1);
        vector<int> cnt(n + 1);
        for (int v : queries) ++cnt[v];
        function<void(int)> dfs = [&](int i) {
            if (i > n) return;
            tree[i] ^= 1;
            dfs(i << 1);
            dfs(i << 1 | 1);
        };
        for (int i = 0; i < n + 1; ++i) {
            if (cnt[i] & 1) {
                dfs(i);
            }
        }
        return accumulate(tree.begin(), tree.end(), 0);
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func numberOfNodes(n int, queries []int) int {
    tree := make([]int, n+1)
    cnt := make([]int, n+1)
    for _, v := range queries {
        cnt[v]++
    }
    var dfs func(int)
    dfs = func(i int) {
        if i > n {
            return
        }
        tree[i] ^= 1
        dfs(i << 1)
        dfs(i<<1 | 1)
    }
    for i, v := range cnt {
        if v%2 == 1 {
            dfs(i)
        }
    }
    ans := 0
    for _, v := range tree {
        ans += v
    }
    return ans
}

Comments