Skip to content

812. Largest Triangle Area

Description

Given an array of points on the X-Y plane points where points[i] = [xi, yi], return the area of the largest triangle that can be formed by any three different points. Answers within 10-5 of the actual answer will be accepted.

 

Example 1:

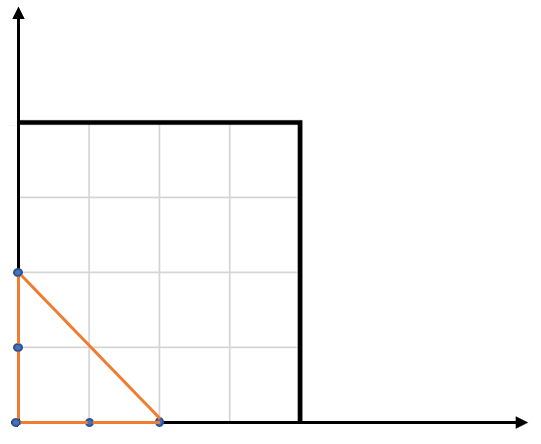
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2.00000
Explanation: The five points are shown in the above figure. The red triangle is the largest.

Example 2:

Input: points = [[1,0],[0,0],[0,1]]
Output: 0.50000

 

Constraints:

  • 3 <= points.length <= 50
  • -50 <= xi, yi <= 50
  • All the given points are unique.

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution:
    def largestTriangleArea(self, points: List[List[int]]) -> float:
        ans = 0
        for x1, y1 in points:
            for x2, y2 in points:
                for x3, y3 in points:
                    u1, v1 = x2 - x1, y2 - y1
                    u2, v2 = x3 - x1, y3 - y1
                    t = abs(u1 * v2 - u2 * v1) / 2
                    ans = max(ans, t)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public double largestTriangleArea(int[][] points) {
        double ans = 0;
        for (int[] p1 : points) {
            int x1 = p1[0], y1 = p1[1];
            for (int[] p2 : points) {
                int x2 = p2[0], y2 = p2[1];
                for (int[] p3 : points) {
                    int x3 = p3[0], y3 = p3[1];
                    int u1 = x2 - x1, v1 = y2 - y1;
                    int u2 = x3 - x1, v2 = y3 - y1;
                    double t = Math.abs(u1 * v2 - u2 * v1) / 2.0;
                    ans = Math.max(ans, t);
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) {
        double ans = 0;
        for (auto& p1 : points) {
            int x1 = p1[0], y1 = p1[1];
            for (auto& p2 : points) {
                int x2 = p2[0], y2 = p2[1];
                for (auto& p3 : points) {
                    int x3 = p3[0], y3 = p3[1];
                    int u1 = x2 - x1, v1 = y2 - y1;
                    int u2 = x3 - x1, v2 = y3 - y1;
                    double t = abs(u1 * v2 - u2 * v1) / 2.0;
                    ans = max(ans, t);
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func largestTriangleArea(points [][]int) float64 {
    ans := 0.0
    for _, p1 := range points {
        x1, y1 := p1[0], p1[1]
        for _, p2 := range points {
            x2, y2 := p2[0], p2[1]
            for _, p3 := range points {
                x3, y3 := p3[0], p3[1]
                u1, v1 := x2-x1, y2-y1
                u2, v2 := x3-x1, y3-y1
                t := float64(abs(u1*v2-u2*v1)) / 2.0
                ans = math.Max(ans, t)
            }
        }
    }
    return ans
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

Comments