787. Cheapest Flights Within K Stops

Description

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.

You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

 

Example 1:

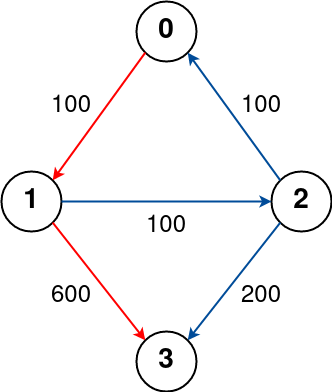
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output: 700
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.

Example 2:

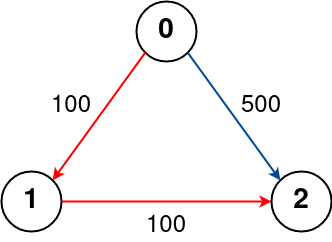
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.

Example 3:

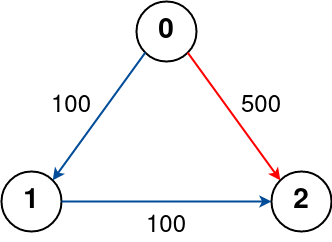
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.

 

Constraints:

• 1 <= n <= 100
• 0 <= flights.length <= (n * (n - 1) / 2)
• flights[i].length == 3
• 0 <= fromi, toi < n
• fromi != toi
• 1 <= pricei <= 104
• There will not be any multiple flights between two cities.
• 0 <= src, dst, k < n
• src != dst

Solutions

Solution 1

Python3JavaC++Go

class Solution:
    def findCheapestPrice(
        self, n: int, flights: List[List[int]], src: int, dst: int, k: int
    ) -> int:
        INF = 0x3F3F3F3F
        dist = [INF] * n
        dist[src] = 0
        for _ in range(k + 1):
            backup = dist.copy()
            for f, t, p in flights:
                dist[t] = min(dist[t], backup[f] + p)
        return -1 if dist[dst] == INF else dist[dst]

class Solution {
    private static final int INF = 0x3f3f3f3f;

    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        int[] dist = new int[n];
        int[] backup = new int[n];
        Arrays.fill(dist, INF);
        dist[src] = 0;
        for (int i = 0; i < k + 1; ++i) {
            System.arraycopy(dist, 0, backup, 0, n);
            for (int[] e : flights) {
                int f = e[0], t = e[1], p = e[2];
                dist[t] = Math.min(dist[t], backup[f] + p);
            }
        }
        return dist[dst] == INF ? -1 : dist[dst];
    }
}

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        const int inf = 0x3f3f3f3f;
        vector<int> dist(n, inf);
        vector<int> backup;
        dist[src] = 0;
        for (int i = 0; i < k + 1; ++i) {
            backup = dist;
            for (auto& e : flights) {
                int f = e[0], t = e[1], p = e[2];
                dist[t] = min(dist[t], backup[f] + p);
            }
        }
        return dist[dst] == inf ? -1 : dist[dst];
    }
};

func findCheapestPrice(n int, flights [][]int, src int, dst int, k int) int {
    const inf = 0x3f3f3f3f
    dist := make([]int, n)
    backup := make([]int, n)
    for i := range dist {
        dist[i] = inf
    }
    dist[src] = 0
    for i := 0; i < k+1; i++ {
        copy(backup, dist)
        for _, e := range flights {
            f, t, p := e[0], e[1], e[2]
            dist[t] = min(dist[t], backup[f]+p)
        }
    }
    if dist[dst] == inf {
        return -1
    }
    return dist[dst]
}

Solution 2

Python3JavaC++Go

class Solution:
    def findCheapestPrice(
        self, n: int, flights: List[List[int]], src: int, dst: int, k: int
    ) -> int:
        @cache
        def dfs(u, k):
            if u == dst:
                return 0
            if k <= 0:
                return inf
            k -= 1
            ans = inf
            for v, p in g[u]:
                ans = min(ans, dfs(v, k) + p)
            return ans

        g = defaultdict(list)
        for u, v, p in flights:
            g[u].append((v, p))
        ans = dfs(src, k + 1)
        return -1 if ans >= inf else ans

class Solution {
    private int[][] memo;
    private int[][] g;
    private int dst;
    private static final int INF = (int) 1e6;

    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        n += 10;
        memo = new int[n][n];
        for (int i = 0; i < n; ++i) {
            Arrays.fill(memo[i], -1);
        }
        g = new int[n][n];
        for (int[] e : flights) {
            g[e[0]][e[1]] = e[2];
        }
        this.dst = dst;
        int ans = dfs(src, k + 1);
        return ans >= INF ? -1 : ans;
    }

    private int dfs(int u, int k) {
        if (memo[u][k] != -1) {
            return memo[u][k];
        }
        if (u == dst) {
            return 0;
        }
        if (k <= 0) {
            return INF;
        }
        int ans = INF;
        for (int v = 0; v < g[u].length; ++v) {
            if (g[u][v] > 0) {
                ans = Math.min(ans, dfs(v, k - 1) + g[u][v]);
            }
        }
        memo[u][k] = ans;
        return ans;
    }
}

class Solution {
public:
    vector<vector<int>> memo;
    vector<vector<int>> g;
    int dst;
    int inf = 1e6;

    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        n += 10;
        memo.resize(n, vector<int>(n, -1));
        g.resize(n, vector<int>(n));
        for (auto& e : flights) g[e[0]][e[1]] = e[2];
        this->dst = dst;
        int ans = dfs(src, k + 1);
        return ans >= inf ? -1 : ans;
    }

    int dfs(int u, int k) {
        if (memo[u][k] != -1) return memo[u][k];
        if (u == dst) return 0;
        if (k <= 0) return inf;
        int ans = inf;
        for (int v = 0; v < g[u].size(); ++v)
            if (g[u][v] > 0)
                ans = min(ans, dfs(v, k - 1) + g[u][v]);
        memo[u][k] = ans;
        return memo[u][k];
    }
};

func findCheapestPrice(n int, flights [][]int, src int, dst int, k int) int {
    n += 10
    memo := make([][]int, n)
    g := make([][]int, n)
    for i := range memo {
        memo[i] = make([]int, n)
        g[i] = make([]int, n)
        for j := range memo[i] {
            memo[i][j] = -1
        }
    }

    for _, e := range flights {
        g[e[0]][e[1]] = e[2]
    }
    inf := int(1e6)
    var dfs func(u, k int) int
    dfs = func(u, k int) int {
        if memo[u][k] != -1 {
            return memo[u][k]
        }
        if u == dst {
            return 0
        }
        if k <= 0 {
            return inf
        }
        ans := inf
        for v, p := range g[u] {
            if p > 0 {
                ans = min(ans, dfs(v, k-1)+p)
            }
        }
        memo[u][k] = ans
        return ans
    }
    ans := dfs(src, k+1)
    if ans >= inf {
        return -1
    }
    return ans
}

Comments