Skip to content

840. Magic Squares In Grid

Description

A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.

Given a row x col grid of integers, how many 3 x 3 magic square subgrids are there?

Note: while a magic square can only contain numbers from 1 to 9, grid may contain numbers up to 15.

 

Example 1:

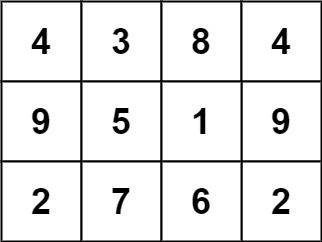
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]]
Output: 1
Explanation: 
The following subgrid is a 3 x 3 magic square:

while this one is not:

In total, there is only one magic square inside the given grid.

Example 2:

Input: grid = [[8]]
Output: 0

 

Constraints:

  • row == grid.length
  • col == grid[i].length
  • 1 <= row, col <= 10
  • 0 <= grid[i][j] <= 15

Solutions

Solution 1: Enumeration

We directly enumerate the top-left coordinates $(i, j)$ of each $3 \times 3$ sub-matrix, then check whether the sub-matrix satisfies the "magic square" condition. If it does, increment the answer by one. After enumeration, return the answer.

Time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively. Space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def numMagicSquaresInside(self, grid: List[List[int]]) -> int:
        def check(i: int, j: int) -> int:
            if i + 3 > m or j + 3 > n:
                return 0
            s = set()
            row = [0] * 3
            col = [0] * 3
            a = b = 0
            for x in range(i, i + 3):
                for y in range(j, j + 3):
                    v = grid[x][y]
                    if v < 1 or v > 9:
                        return 0
                    s.add(v)
                    row[x - i] += v
                    col[y - j] += v
                    if x - i == y - j:
                        a += v
                    if x - i == 2 - (y - j):
                        b += v
            if len(s) != 9 or a != b:
                return 0
            if any(x != a for x in row) or any(x != a for x in col):
                return 0
            return 1

        m, n = len(grid), len(grid[0])
        return sum(check(i, j) for i in range(m) for j in range(n))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution {
    private int m;
    private int n;
    private int[][] grid;

    public int numMagicSquaresInside(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        this.grid = grid;
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                ans += check(i, j);
            }
        }
        return ans;
    }

    private int check(int i, int j) {
        if (i + 3 > m || j + 3 > n) {
            return 0;
        }
        int[] cnt = new int[16];
        int[] row = new int[3];
        int[] col = new int[3];
        int a = 0, b = 0;
        for (int x = i; x < i + 3; ++x) {
            for (int y = j; y < j + 3; ++y) {
                int v = grid[x][y];
                if (v < 1 || v > 9 || ++cnt[v] > 1) {
                    return 0;
                }
                row[x - i] += v;
                col[y - j] += v;
                if (x - i == y - j) {
                    a += v;
                }
                if (x - i + y - j == 2) {
                    b += v;
                }
            }
        }
        if (a != b) {
            return 0;
        }
        for (int k = 0; k < 3; ++k) {
            if (row[k] != a || col[k] != a) {
                return 0;
            }
        }
        return 1;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    int numMagicSquaresInside(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        int ans = 0;
        auto check = [&](int i, int j) {
            if (i + 3 > m || j + 3 > n) {
                return 0;
            }
            vector<int> cnt(16);
            vector<int> row(3);
            vector<int> col(3);
            int a = 0, b = 0;
            for (int x = i; x < i + 3; ++x) {
                for (int y = j; y < j + 3; ++y) {
                    int v = grid[x][y];
                    if (v < 1 || v > 9 || ++cnt[v] > 1) {
                        return 0;
                    }
                    row[x - i] += v;
                    col[y - j] += v;
                    if (x - i == y - j) {
                        a += v;
                    }
                    if (x - i + y - j == 2) {
                        b += v;
                    }
                }
            }
            if (a != b) {
                return 0;
            }
            for (int k = 0; k < 3; ++k) {
                if (row[k] != a || col[k] != a) {
                    return 0;
                }
            }
            return 1;
        };
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                ans += check(i, j);
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
func numMagicSquaresInside(grid [][]int) (ans int) {
    m, n := len(grid), len(grid[0])
    check := func(i, j int) int {
        if i+3 > m || j+3 > n {
            return 0
        }
        cnt := [16]int{}
        row := [3]int{}
        col := [3]int{}
        a, b := 0, 0
        for x := i; x < i+3; x++ {
            for y := j; y < j+3; y++ {
                v := grid[x][y]
                if v < 1 || v > 9 || cnt[v] > 0 {
                    return 0
                }
                cnt[v]++
                row[x-i] += v
                col[y-j] += v
                if x-i == y-j {
                    a += v
                }
                if x-i == 2-(y-j) {
                    b += v
                }
            }
        }
        if a != b {
            return 0
        }
        for k := 0; k < 3; k++ {
            if row[k] != a || col[k] != a {
                return 0
            }
        }
        return 1
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            ans += check(i, j)
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
function numMagicSquaresInside(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const check = (i: number, j: number): number => {
        if (i + 3 > m || j + 3 > n) {
            return 0;
        }
        const cnt: number[] = Array(16).fill(0);
        const row: number[] = Array(3).fill(0);
        const col: number[] = Array(3).fill(0);
        let [a, b] = [0, 0];
        for (let x = i; x < i + 3; ++x) {
            for (let y = j; y < j + 3; ++y) {
                const v = grid[x][y];
                if (v < 1 || v > 9 || ++cnt[v] > 1) {
                    return 0;
                }
                row[x - i] += v;
                col[y - j] += v;
                if (x - i === y - j) {
                    a += v;
                }
                if (x - i === 2 - (y - j)) {
                    b += v;
                }
            }
        }
        if (a !== b) {
            return 0;
        }
        for (let k = 0; k < 3; ++k) {
            if (row[k] !== a || col[k] !== a) {
                return 0;
            }
        }
        return 1;
    };
    let ans = 0;
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            ans += check(i, j);
        }
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
function numMagicSquaresInside(grid) {
    const m = grid.length;
    const n = grid[0].length;
    const check = (i, j) => {
        if (i + 3 > m || j + 3 > n) {
            return 0;
        }
        const cnt = Array(16).fill(0);
        const row = Array(3).fill(0);
        const col = Array(3).fill(0);
        let [a, b] = [0, 0];
        for (let x = i; x < i + 3; ++x) {
            for (let y = j; y < j + 3; ++y) {
                const v = grid[x][y];
                if (v < 1 || v > 9 || ++cnt[v] > 1) {
                    return 0;
                }
                row[x - i] += v;
                col[y - j] += v;
                if (x - i === y - j) {
                    a += v;
                }
                if (x - i === 2 - (y - j)) {
                    b += v;
                }
            }
        }
        if (a !== b) {
            return 0;
        }
        for (let k = 0; k < 3; ++k) {
            if (row[k] !== a || col[k] !== a) {
                return 0;
            }
        }
        return 1;
    };
    let ans = 0;
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            ans += check(i, j);
        }
    }
    return ans;
}

Solution 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
export function numMagicSquaresInside(grid: number[][]): number {
    const [m, n] = [grid.length, grid[0].length];
    if (m < 3 || n < 3) return 0;

    const check = (y: number, x: number) => {
        const g = grid;
        if (g[y + 1][x + 1] !== 5) return 0;

        const cells = [
            g[y][x],
            g[y][x + 1],
            g[y][x + 2],
            g[y + 1][x + 2],
            g[y + 2][x + 2],
            g[y + 2][x + 1],
            g[y + 2][x],
            g[y + 1][x],
        ];

        const i = cells.indexOf(2);
        if (i === -1) return 0;
        cells.push(...cells.splice(0, i));

        const circle = [2, 9, 4, 3, 8, 1, 6, 7];
        const reverseCircle = [2, 7, 6, 1, 8, 3, 4, 9];

        if (cells.every((x, i) => x === circle[i])) return 1;
        if (cells.every((x, i) => x === reverseCircle[i])) return 1;

        return 0;
    };

    let res = 0;
    for (let i = 0; i < m - 2; i++) {
        for (let j = 0; j < n - 2; j++) {
            res += check(i, j);
        }
    }

    return res;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
function numMagicSquaresInside(grid) {
    const [m, n] = [grid.length, grid[0].length];
    if (m < 3 || n < 3) return 0;

    const check = (y, x) => {
        const g = grid;
        if (g[y + 1][x + 1] !== 5) return false;

        const cells = [
            g[y][x],
            g[y][x + 1],
            g[y][x + 2],
            g[y + 1][x + 2],
            g[y + 2][x + 2],
            g[y + 2][x + 1],
            g[y + 2][x],
            g[y + 1][x],
        ];

        const i = cells.indexOf(2);
        if (i === -1) return false;
        cells.push(...cells.splice(0, i));

        const circle = [2, 9, 4, 3, 8, 1, 6, 7];
        const reverseCircle = [2, 7, 6, 1, 8, 3, 4, 9];

        if (cells.every((x, i) => x === circle[i])) return true;
        if (cells.every((x, i) => x === reverseCircle[i])) return true;

        return false;
    };

    let res = 0;
    for (let i = 0; i < m - 2; i++) {
        for (let j = 0; j < n - 2; j++) {
            res += +check(i, j);
        }
    }

    return res;
}

Comments