Skip to content

2714. Find Shortest Path with K Hops πŸ”’

Description

You are given a positive integer n which is the number of nodes of a 0-indexed undirected weighted connected graph and a 0-indexed 2D array edges where edges[i] = [ui, vi, wi] indicates that there is an edge between nodes ui and vi with weight wi.

You are also given two nodes s and d, and a positive integer k, your task is to find the shortest path from s to d, but you can hop over at most k edges. In other words, make the weight of at most k edges 0 and then find the shortest path from s to d.

Return the length of the shortest path from s to d with the given condition.

 

Example 1:

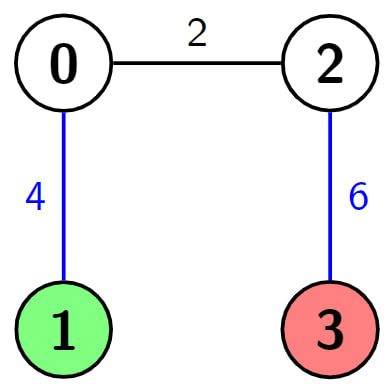
Input: n = 4, edges = [[0,1,4],[0,2,2],[2,3,6]], s = 1, d = 3, k = 2
Output: 2
Explanation: In this example there is only one path from node 1 (the green node) to node 3 (the red node), which is (1->0->2->3) and the length of it is 4 + 2 + 6 = 12. Now we can make weight of two edges 0, we make weight of the blue edges 0, then we have 0 + 2 + 0 = 2. It can be shown that 2 is the minimum length of a path we can achieve with the given condition.

Example 2:

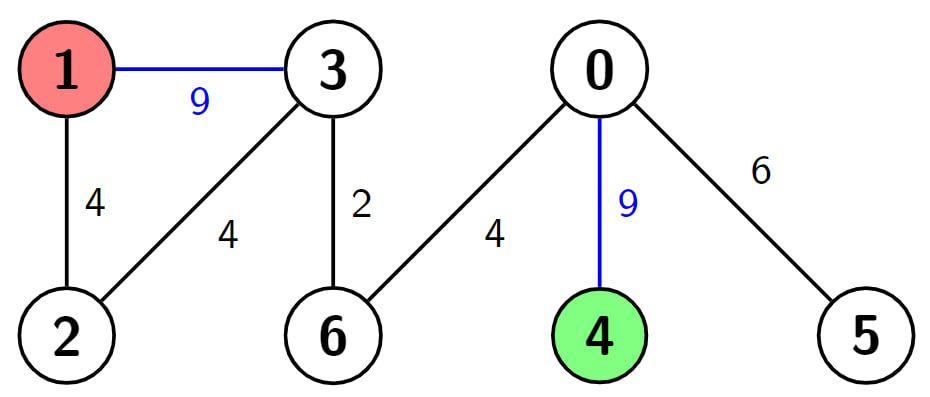
Input: n = 7, edges = [[3,1,9],[3,2,4],[4,0,9],[0,5,6],[3,6,2],[6,0,4],[1,2,4]], s = 4, d = 1, k = 2
Output: 6
Explanation: In this example there are 2 paths from node 4 (the green node) to node 1 (the red node), which are (4->0->6->3->2->1) and (4->0->6->3->1). The first one has the length 9 + 4 + 2 + 4 + 4 = 23, and the second one has the length 9 + 4 + 2 + 9 = 24. Now if we make weight of the blue edges 0, we get the shortest path with the length 0 + 4 + 2 + 0 = 6. It can be shown that 6 is the minimum length of a path we can achieve with the given condition.

Example 3:

Input: n = 5, edges = [[0,4,2],[0,1,3],[0,2,1],[2,1,4],[1,3,4],[3,4,7]], s = 2, d = 3, k = 1
Output: 3
Explanation: In this example there are 4 paths from node 2 (the green node) to node 3 (the red node), which are (2->1->3), (2->0->1->3), (2->1->0->4->3) and (2->0->4->3). The first two have the length 4 + 4 = 1 + 3 + 4 = 8, the third one has the length 4 + 3 + 2 + 7 = 16 and the last one has the length 1 + 2 + 7 = 10. Now if we make weight of the blue edge 0, we get the shortest path with the length 1 + 2 + 0 = 3. It can be shown that 3 is the minimum length of a path we can achieve with the given condition.

 

Constraints:

  • 2 <= n <= 500
  • n - 1 <= edges.length <= min(104, n * (n - 1) / 2)
  • edges[i].length = 3
  • 0 <= edges[i][0], edges[i][1] <= n - 1
  • 1 <= edges[i][2] <= 106
  • 0 <= s, d, k <= n - 1
  • s != d
  • The input is generated such that the graph is connected and has no repeated edges or self-loops

Solutions

Solution 1: Dijkstra Algorithm

First, we construct a graph \(g\) based on the given edges, where \(g[u]\) represents all neighboring nodes of node \(u\) and their corresponding edge weights.

Then, we use Dijkstra's algorithm to find the shortest path from node \(s\) to node \(d\). However, we need to make some modifications to Dijkstra's algorithm:

  • We need to record the shortest path length from each node \(u\) to node \(d\), but since we can cross at most \(k\) edges, we need to record the shortest path length from each node \(u\) to node \(d\) and the number of edges crossed \(t\), i.e., \(dist[u][t]\) represents the shortest path length from node \(u\) to node \(d\) and the number of edges crossed is \(t\).
  • We need to use a priority queue to maintain the current shortest path, but since we need to record the number of edges crossed, we need to use a triple \((dis, u, t)\) to represent the current shortest path, where \(dis\) represents the current shortest path length, and \(u\) and \(t\) represent the current node and the number of edges crossed, respectively.

Finally, we only need to return the minimum value in \(dist[d][0..k]\).

The time complexity is \(O(n^2 \times \log n)\), and the space complexity is \(O(n \times k)\), where \(n\) represents the number of nodes and \(k\) represents the maximum number of edges crossed.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def shortestPathWithHops(
        self, n: int, edges: List[List[int]], s: int, d: int, k: int
    ) -> int:
        g = [[] for _ in range(n)]
        for u, v, w in edges:
            g[u].append((v, w))
            g[v].append((u, w))
        dist = [[inf] * (k + 1) for _ in range(n)]
        dist[s][0] = 0
        pq = [(0, s, 0)]
        while pq:
            dis, u, t = heappop(pq)
            for v, w in g[u]:
                if t + 1 <= k and dist[v][t + 1] > dis:
                    dist[v][t + 1] = dis
                    heappush(pq, (dis, v, t + 1))
                if dist[v][t] > dis + w:
                    dist[v][t] = dis + w
                    heappush(pq, (dis + w, v, t))
        return int(min(dist[d]))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public int shortestPathWithHops(int n, int[][] edges, int s, int d, int k) {
        List<int[]>[] g = new List[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int[] e : edges) {
            int u = e[0], v = e[1], w = e[2];
            g[u].add(new int[] {v, w});
            g[v].add(new int[] {u, w});
        }
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        pq.offer(new int[] {0, s, 0});
        int[][] dist = new int[n][k + 1];
        final int inf = 1 << 30;
        for (int[] e : dist) {
            Arrays.fill(e, inf);
        }
        dist[s][0] = 0;
        while (!pq.isEmpty()) {
            int[] p = pq.poll();
            int dis = p[0], u = p[1], t = p[2];
            for (int[] e : g[u]) {
                int v = e[0], w = e[1];
                if (t + 1 <= k && dist[v][t + 1] > dis) {
                    dist[v][t + 1] = dis;
                    pq.offer(new int[] {dis, v, t + 1});
                }
                if (dist[v][t] > dis + w) {
                    dist[v][t] = dis + w;
                    pq.offer(new int[] {dis + w, v, t});
                }
            }
        }
        int ans = inf;
        for (int i = 0; i <= k; ++i) {
            ans = Math.min(ans, dist[d][i]);
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int shortestPathWithHops(int n, vector<vector<int>>& edges, int s, int d, int k) {
        vector<pair<int, int>> g[n];
        for (auto& e : edges) {
            int u = e[0], v = e[1], w = e[2];
            g[u].emplace_back(v, w);
            g[v].emplace_back(u, w);
        }
        priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> pq;
        pq.emplace(0, s, 0);
        int dist[n][k + 1];
        memset(dist, 0x3f, sizeof(dist));
        dist[s][0] = 0;
        while (!pq.empty()) {
            auto [dis, u, t] = pq.top();
            pq.pop();
            for (auto [v, w] : g[u]) {
                if (t + 1 <= k && dist[v][t + 1] > dis) {
                    dist[v][t + 1] = dis;
                    pq.emplace(dis, v, t + 1);
                }
                if (dist[v][t] > dis + w) {
                    dist[v][t] = dis + w;
                    pq.emplace(dis + w, v, t);
                }
            }
        }
        return *min_element(dist[d], dist[d] + k + 1);
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
func shortestPathWithHops(n int, edges [][]int, s int, d int, k int) int {
    g := make([][][2]int, n)
    for _, e := range edges {
        u, v, w := e[0], e[1], e[2]
        g[u] = append(g[u], [2]int{v, w})
        g[v] = append(g[v], [2]int{u, w})
    }
    pq := hp{{0, s, 0}}
    dist := make([][]int, n)
    for i := range dist {
        dist[i] = make([]int, k+1)
        for j := range dist[i] {
            dist[i][j] = math.MaxInt32
        }
    }
    dist[s][0] = 0
    for len(pq) > 0 {
        p := heap.Pop(&pq).(tuple)
        dis, u, t := p.dis, p.u, p.t
        for _, e := range g[u] {
            v, w := e[0], e[1]
            if t+1 <= k && dist[v][t+1] > dis {
                dist[v][t+1] = dis
                heap.Push(&pq, tuple{dis, v, t + 1})
            }
            if dist[v][t] > dis+w {
                dist[v][t] = dis + w
                heap.Push(&pq, tuple{dis + w, v, t})
            }
        }
    }
    return slices.Min(dist[d])
}

type tuple struct{ dis, u, t int }
type hp []tuple

func (h hp) Len() int           { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].dis < h[j].dis }
func (h hp) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any)        { *h = append(*h, v.(tuple)) }
func (h *hp) Pop() any          { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }

Comments