174. Dungeon Game

Description

The demons had captured the princess and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of m x n rooms laid out in a 2D grid. Our valiant knight was initially positioned in the top-left room and must fight his way through dungeon to rescue the princess.

The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.

Some of the rooms are guarded by demons (represented by negative integers), so the knight loses health upon entering these rooms; other rooms are either empty (represented as 0) or contain magic orbs that increase the knight's health (represented by positive integers).

To reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

Return the knight's minimum initial health so that he can rescue the princess.

Note that any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.

Example 1:

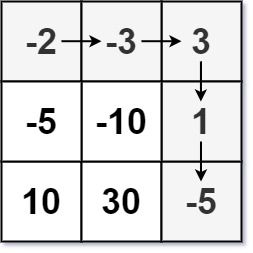
Input: dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
Output: 7
Explanation: The initial health of the knight must be at least 7 if he follows the optimal path: RIGHT-> RIGHT -> DOWN -> DOWN.

Example 2:

Input: dungeon = [[0]]
Output: 1

Constraints:

m == dungeon.length
n == dungeon[i].length
1 <= m, n <= 200
-1000 <= dungeon[i][j] <= 1000

Solutions

Solution 1: Dynamic Programming

We define $dp[i][j]$ as the minimum initial value needed from $(i, j)$ to the end point. The value of $dp[i][j]$ can be obtained from $dp[i+1][j]$ and $dp[i][j+1]$, that is:

$$ dp[i][j] = \max(\min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j], 1) $$

Initially, $dp[m][n-1]$ and $dp[m-1][n]$ are both $1$, and the values at other positions are maximum.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Where $m$ and $n$ are the number of rows and columns of the dungeon, respectively.

Python3JavaC++GoC#

class Solution:
    def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:
        m, n = len(dungeon), len(dungeon[0])
        dp = [[inf] * (n + 1) for _ in range(m + 1)]
        dp[m][n - 1] = dp[m - 1][n] = 1
        for i in range(m - 1, -1, -1):
            for j in range(n - 1, -1, -1):
                dp[i][j] = max(1, min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j])
        return dp[0][0]

class Solution {
    public int calculateMinimumHP(int[][] dungeon) {
        int m = dungeon.length, n = dungeon[0].length;
        int[][] dp = new int[m + 1][n + 1];
        for (var e : dp) {
            Arrays.fill(e, 1 << 30);
        }
        dp[m][n - 1] = dp[m - 1][n] = 1;
        for (int i = m - 1; i >= 0; --i) {
            for (int j = n - 1; j >= 0; --j) {
                dp[i][j] = Math.max(1, Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]);
            }
        }
        return dp[0][0];
    }
}

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m = dungeon.size(), n = dungeon[0].size();
        int dp[m + 1][n + 1];
        memset(dp, 0x3f, sizeof dp);
        dp[m][n - 1] = dp[m - 1][n] = 1;
        for (int i = m - 1; ~i; --i) {
            for (int j = n - 1; ~j; --j) {
                dp[i][j] = max(1, min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]);
            }
        }
        return dp[0][0];
    }
};

func calculateMinimumHP(dungeon [][]int) int {
    m, n := len(dungeon), len(dungeon[0])
    dp := make([][]int, m+1)
    for i := range dp {
        dp[i] = make([]int, n+1)
        for j := range dp[i] {
            dp[i][j] = 1 << 30
        }
    }
    dp[m][n-1], dp[m-1][n] = 1, 1
    for i := m - 1; i >= 0; i-- {
        for j := n - 1; j >= 0; j-- {
            dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1])-dungeon[i][j])
        }
    }
    return dp[0][0]
}

public class Solution {
    public int CalculateMinimumHP(int[][] dungeon) {
        int m = dungeon.Length, n = dungeon[0].Length;
        int[][] dp = new int[m + 1][];
        for (int i = 0; i < m + 1; ++i) {
            dp[i] = new int[n + 1];
            Array.Fill(dp[i], 1 << 30);
        }
        dp[m][n - 1] = dp[m - 1][n] = 1;
        for (int i = m - 1; i >= 0; --i) {
            for (int j = n - 1; j >= 0; --j) {
                dp[i][j] = Math.Max(1, Math.Min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]);
            }
        }
        return dp[0][0];
    }
}

174. Dungeon Game

Description

Solutions

Solution 1: Dynamic Programming

Comments