Skip to content

2251. Number of Flowers in Full Bloom

Description

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [starti, endi] means the ith flower will be in full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the ith person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.

 

Example 1:

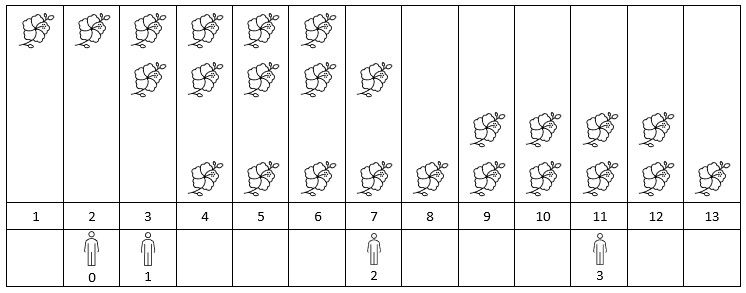
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

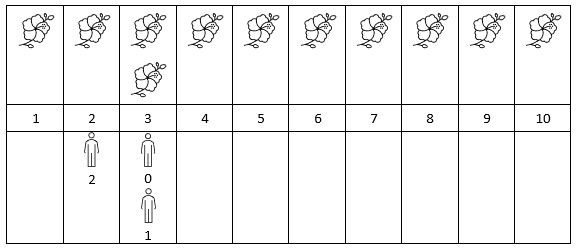
Input: flowers = [[1,10],[3,3]], people = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

 

Constraints:

  • 1 <= flowers.length <= 5 * 104
  • flowers[i].length == 2
  • 1 <= starti <= endi <= 109
  • 1 <= people.length <= 5 * 104
  • 1 <= people[i] <= 109

Solutions

Solution 1

1
2
3
4
5
6
class Solution:
    def fullBloomFlowers(
        self, flowers: List[List[int]], people: List[int]
    ) -> List[int]:
        start, end = sorted(a for a, _ in flowers), sorted(b for _, b in flowers)
        return [bisect_right(start, p) - bisect_left(end, p) for p in people]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int[] fullBloomFlowers(int[][] flowers, int[] people) {
        int n = flowers.length;
        int[] start = new int[n];
        int[] end = new int[n];
        for (int i = 0; i < n; ++i) {
            start[i] = flowers[i][0];
            end[i] = flowers[i][1];
        }
        Arrays.sort(start);
        Arrays.sort(end);
        int m = people.length;
        int[] ans = new int[m];
        for (int i = 0; i < m; ++i) {
            ans[i] = search(start, people[i] + 1) - search(end, people[i]);
        }
        return ans;
    }

    private int search(int[] nums, int x) {
        int l = 0, r = nums.length;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (nums[mid] >= x) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return l;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {
        int n = flowers.size();
        vector<int> start;
        vector<int> end;
        for (auto& f : flowers) {
            start.push_back(f[0]);
            end.push_back(f[1]);
        }
        sort(start.begin(), start.end());
        sort(end.begin(), end.end());
        vector<int> ans;
        for (auto& p : people) {
            auto r = upper_bound(start.begin(), start.end(), p) - start.begin();
            auto l = lower_bound(end.begin(), end.end(), p) - end.begin();
            ans.push_back(r - l);
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
func fullBloomFlowers(flowers [][]int, people []int) (ans []int) {
    n := len(flowers)
    start := make([]int, n)
    end := make([]int, n)
    for i, f := range flowers {
        start[i] = f[0]
        end[i] = f[1]
    }
    sort.Ints(start)
    sort.Ints(end)
    for _, p := range people {
        r := sort.SearchInts(start, p+1)
        l := sort.SearchInts(end, p)
        ans = append(ans, r-l)
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
function fullBloomFlowers(flowers: number[][], people: number[]): number[] {
    const n = flowers.length;
    const start = new Array(n).fill(0);
    const end = new Array(n).fill(0);
    for (let i = 0; i < n; ++i) {
        start[i] = flowers[i][0];
        end[i] = flowers[i][1];
    }
    start.sort((a, b) => a - b);
    end.sort((a, b) => a - b);
    const ans: number[] = [];
    for (const p of people) {
        const r = search(start, p + 1);
        const l = search(end, p);
        ans.push(r - l);
    }
    return ans;
}

function search(nums: number[], x: number): number {
    let l = 0;
    let r = nums.length;
    while (l < r) {
        const mid = (l + r) >> 1;
        if (nums[mid] >= x) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    return l;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
use std::collections::BTreeMap;

impl Solution {
    #[allow(dead_code)]
    pub fn full_bloom_flowers(flowers: Vec<Vec<i32>>, people: Vec<i32>) -> Vec<i32> {
        let n = people.len();

        // First sort the people vector based on the first item
        let mut people: Vec<(usize, i32)> = people.into_iter().enumerate().map(|x| x).collect();

        people.sort_by(|lhs, rhs| lhs.1.cmp(&rhs.1));

        // Initialize the difference vector
        let mut diff = BTreeMap::new();
        let mut ret = vec![0; n];

        for f in flowers {
            let (left, right) = (f[0], f[1]);
            diff.entry(left)
                .and_modify(|x| {
                    *x += 1;
                })
                .or_insert(1);

            diff.entry(right + 1)
                .and_modify(|x| {
                    *x -= 1;
                })
                .or_insert(-1);
        }

        let mut sum = 0;
        let mut i = 0;
        for (k, v) in diff {
            while i < n && people[i].1 < k {
                ret[people[i].0] += sum;
                i += 1;
            }
            sum += v;
        }

        ret
    }
}

Solution 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution:
    def fullBloomFlowers(
        self, flowers: List[List[int]], people: List[int]
    ) -> List[int]:
        d = defaultdict(int)
        for st, ed in flowers:
            d[st] += 1
            d[ed + 1] -= 1
        ts = sorted(d)
        s = i = 0
        m = len(people)
        ans = [0] * m
        for t, j in sorted(zip(people, range(m))):
            while i < len(ts) and ts[i] <= t:
                s += d[ts[i]]
                i += 1
            ans[j] = s
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int[] fullBloomFlowers(int[][] flowers, int[] people) {
        TreeMap<Integer, Integer> d = new TreeMap<>();
        for (int[] f : flowers) {
            d.merge(f[0], 1, Integer::sum);
            d.merge(f[1] + 1, -1, Integer::sum);
        }
        int s = 0;
        int m = people.length;
        Integer[] idx = new Integer[m];
        for (int i = 0; i < m; i++) {
            idx[i] = i;
        }
        Arrays.sort(idx, Comparator.comparingInt(i -> people[i]));
        int[] ans = new int[m];
        for (int i : idx) {
            int t = people[i];
            while (!d.isEmpty() && d.firstKey() <= t) {
                s += d.pollFirstEntry().getValue();
            }
            ans[i] = s;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {
        map<int, int> d;
        for (auto& f : flowers) {
            d[f[0]]++;
            d[f[1] + 1]--;
        }
        int m = people.size();
        vector<int> idx(m);
        iota(idx.begin(), idx.end(), 0);
        sort(idx.begin(), idx.end(), [&](int i, int j) {
            return people[i] < people[j];
        });
        vector<int> ans(m);
        int s = 0;
        for (int i : idx) {
            int t = people[i];
            while (!d.empty() && d.begin()->first <= t) {
                s += d.begin()->second;
                d.erase(d.begin());
            }
            ans[i] = s;
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func fullBloomFlowers(flowers [][]int, people []int) []int {
    d := map[int]int{}
    for _, f := range flowers {
        d[f[0]]++
        d[f[1]+1]--
    }
    ts := []int{}
    for t := range d {
        ts = append(ts, t)
    }
    sort.Ints(ts)
    m := len(people)
    idx := make([]int, m)
    for i := range idx {
        idx[i] = i
    }
    sort.Slice(idx, func(i, j int) bool { return people[idx[i]] < people[idx[j]] })
    ans := make([]int, m)
    s, i := 0, 0
    for _, j := range idx {
        t := people[j]
        for i < len(ts) && ts[i] <= t {
            s += d[ts[i]]
            i++
        }
        ans[j] = s
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
function fullBloomFlowers(flowers: number[][], people: number[]): number[] {
    const d: Map<number, number> = new Map();
    for (const [st, ed] of flowers) {
        d.set(st, (d.get(st) || 0) + 1);
        d.set(ed + 1, (d.get(ed + 1) || 0) - 1);
    }
    const ts = [...d.keys()].sort((a, b) => a - b);
    let s = 0;
    let i = 0;
    const m = people.length;
    const idx: number[] = [...Array(m)].map((_, i) => i).sort((a, b) => people[a] - people[b]);
    const ans = Array(m).fill(0);
    for (const j of idx) {
        const t = people[j];
        while (i < ts.length && ts[i] <= t) {
            s += d.get(ts[i])!;
            ++i;
        }
        ans[j] = s;
    }
    return ans;
}

Comments