2397. Maximum Rows Covered by Columns

Description

You are given an m x n binary matrix matrix and an integer numSelect.

Your goal is to select exactly numSelect distinct columns from matrix such that you cover as many rows as possible.

A row is considered covered if all the 1's in that row are also part of a column that you have selected. If a row does not have any 1s, it is also considered covered.

More formally, let us consider selected = {c1, c2, ...., cnumSelect} as the set of columns selected by you. A row i is covered by selected if:

• For each cell where matrix[i][j] == 1, the column j is in selected.
• Or, no cell in row i has a value of 1.

Return the maximum number of rows that can be covered by a set of numSelect columns.

 

Example 1:

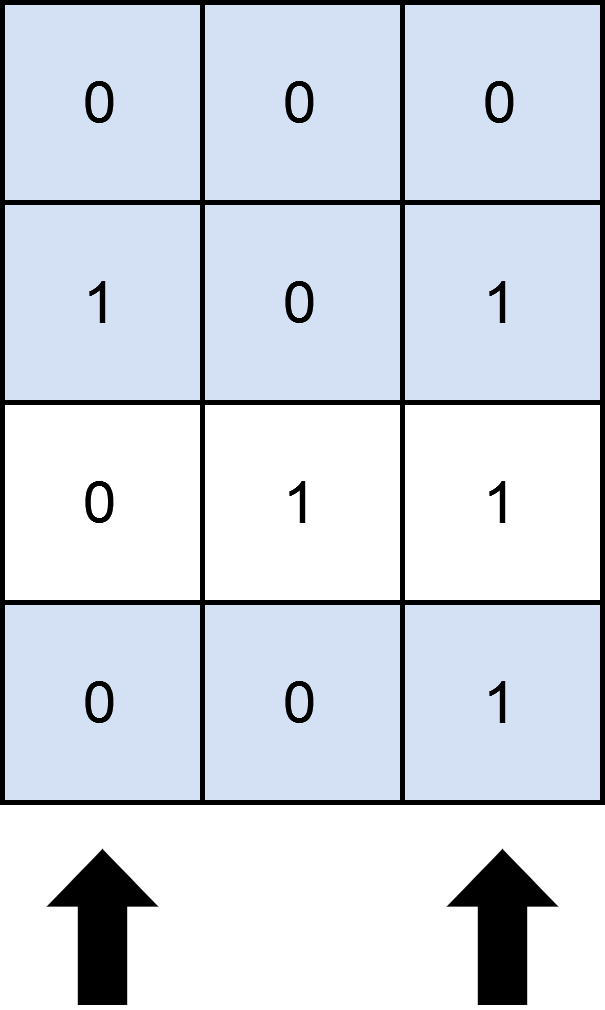
Input: matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2

Output: 3

Explanation:

One possible way to cover 3 rows is shown in the diagram above.
We choose s = {0, 2}.
- Row 0 is covered because it has no occurrences of 1.
- Row 1 is covered because the columns with value 1, i.e. 0 and 2 are present in s.
- Row 2 is not covered because matrix[2][1] == 1 but 1 is not present in s.
- Row 3 is covered because matrix[2][2] == 1 and 2 is present in s.
Thus, we can cover three rows.
Note that s = {1, 2} will also cover 3 rows, but it can be shown that no more than three rows can be covered.

Example 2:

Input: matrix = [[1],[0]], numSelect = 1

Output: 2

Explanation:

Selecting the only column will result in both rows being covered since the entire matrix is selected.

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 12
• matrix[i][j] is either 0 or 1.
• 1 <= numSelect <= n

Solutions

Solution 1: Binary Enumeration

First, we convert each row of the matrix into a binary number and record it in the array $rows$. Here, $rows[i]$ represents the binary number corresponding to the $i$-th row, and the $j$-th bit of this binary number $rows[i]$ represents the value of the $i$-th row and $j$-th column.

Next, we enumerate all $2^n$ column selection schemes, where $n$ is the number of columns in the matrix. For each column selection scheme, we check whether numSelect columns have been selected. If not, we skip it. Otherwise, we count how many rows in the matrix are covered by the selected columns, i.e., how many binary numbers $rows[i]$ are equal to the bitwise AND of $rows[i]$ and the column selection scheme $mask$. We then update the maximum number of rows.

The time complexity is $O(2^n \times m)$, and the space complexity is $O(m)$. Where $m$ and $n$ are the number of rows and columns in the matrix, respectively.

Python3JavaC++GoTypeScript

class Solution:
    def maximumRows(self, matrix: List[List[int]], numSelect: int) -> int:
        rows = []
        for row in matrix:
            mask = reduce(or_, (1 << j for j, x in enumerate(row) if x), 0)
            rows.append(mask)

        ans = 0
        for mask in range(1 << len(matrix[0])):
            if mask.bit_count() != numSelect:
                continue
            t = sum((x & mask) == x for x in rows)
            ans = max(ans, t)
        return ans

class Solution {
    public int maximumRows(int[][] matrix, int numSelect) {
        int m = matrix.length, n = matrix[0].length;
        int[] rows = new int[m];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 1) {
                    rows[i] |= 1 << j;
                }
            }
        }
        int ans = 0;
        for (int mask = 1; mask < 1 << n; ++mask) {
            if (Integer.bitCount(mask) != numSelect) {
                continue;
            }
            int t = 0;
            for (int x : rows) {
                if ((x & mask) == x) {
                    ++t;
                }
            }
            ans = Math.max(ans, t);
        }
        return ans;
    }
}

class Solution {
public:
    int maximumRows(vector<vector<int>>& matrix, int numSelect) {
        int m = matrix.size(), n = matrix[0].size();
        int rows[m];
        memset(rows, 0, sizeof(rows));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j]) {
                    rows[i] |= 1 << j;
                }
            }
        }
        int ans = 0;
        for (int mask = 1; mask < 1 << n; ++mask) {
            if (__builtin_popcount(mask) != numSelect) {
                continue;
            }
            int t = 0;
            for (int x : rows) {
                t += (x & mask) == x;
            }
            ans = max(ans, t);
        }
        return ans;
    }
};

func maximumRows(matrix [][]int, numSelect int) (ans int) {
    m, n := len(matrix), len(matrix[0])
    rows := make([]int, m)
    for i, row := range matrix {
        for j, x := range row {
            if x == 1 {
                rows[i] |= 1 << j
            }
        }
    }
    for mask := 1; mask < 1<<n; mask++ {
        if bits.OnesCount(uint(mask)) != numSelect {
            continue
        }
        t := 0
        for _, x := range rows {
            if (x & mask) == x {
                t++
            }
        }
        if ans < t {
            ans = t
        }
    }
    return
}

function maximumRows(matrix: number[][], numSelect: number): number {
    const [m, n] = [matrix.length, matrix[0].length];
    const rows: number[] = Array(m).fill(0);
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (matrix[i][j]) {
                rows[i] |= 1 << j;
            }
        }
    }
    let ans = 0;
    for (let mask = 1; mask < 1 << n; ++mask) {
        if (bitCount(mask) !== numSelect) {
            continue;
        }
        let t = 0;
        for (const x of rows) {
            if ((x & mask) === x) {
                ++t;
            }
        }
        ans = Math.max(ans, t);
    }
    return ans;
}

function bitCount(i: number): number {
    i = i - ((i >>> 1) & 0x55555555);
    i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
    i = (i + (i >>> 4)) & 0x0f0f0f0f;
    i = i + (i >>> 8);
    i = i + (i >>> 16);
    return i & 0x3f;
}

Comments