Skip to content

1245. Tree Diameter πŸ”’

Description

The diameter of a tree is the number of edges in the longest path in that tree.

There is an undirected tree of n nodes labeled from 0 to n - 1. You are given a 2D array edges where edges.length == n - 1 and edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the tree.

Return the diameter of the tree.

 

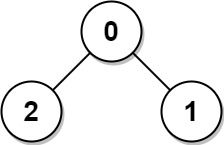
Example 1:

Input: edges = [[0,1],[0,2]]
Output: 2
Explanation: The longest path of the tree is the path 1 - 0 - 2.

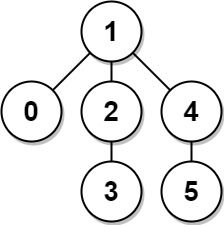
Example 2:

Input: edges = [[0,1],[1,2],[2,3],[1,4],[4,5]]
Output: 4
Explanation: The longest path of the tree is the path 3 - 2 - 1 - 4 - 5.

 

Constraints:

  • n == edges.length + 1
  • 1 <= n <= 104
  • 0 <= ai, bi < n
  • ai != bi

Solutions

Solution 1: Two DFS Passes

First, we arbitrarily select a node and start a depth-first search (DFS) from this node to find the farthest node from it, denoted as node $a$. Then, we start another DFS from node $a$ to find the farthest node from node $a$, denoted as node $b$. It can be proven that the path between node $a$ and node $b$ is the diameter of the tree.

Time complexity is $O(n)$, and space complexity is $O(n)$, where $n$ is the number of nodes.

Similar problems:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def treeDiameter(self, edges: List[List[int]]) -> int:
        def dfs(i: int, fa: int, t: int):
            for j in g[i]:
                if j != fa:
                    dfs(j, i, t + 1)
            nonlocal ans, a
            if ans < t:
                ans = t
                a = i

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        ans = a = 0
        dfs(0, -1, 0)
        dfs(a, -1, 0)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    private List<Integer>[] g;
    private int ans;
    private int a;

    public int treeDiameter(int[][] edges) {
        int n = edges.length + 1;
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs(0, -1, 0);
        dfs(a, -1, 0);
        return ans;
    }

    private void dfs(int i, int fa, int t) {
        for (int j : g[i]) {
            if (j != fa) {
                dfs(j, i, t + 1);
            }
        }
        if (ans < t) {
            ans = t;
            a = i;
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int treeDiameter(vector<vector<int>>& edges) {
        int n = edges.size() + 1;
        vector<int> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        int ans = 0, a = 0;
        auto dfs = [&](auto&& dfs, int i, int fa, int t) -> void {
            for (int j : g[i]) {
                if (j != fa) {
                    dfs(dfs, j, i, t + 1);
                }
            }
            if (ans < t)