1552. Magnetic Force Between Two Balls

Description

In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the i^th basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum.

Rick stated that magnetic force between two different balls at positions x and y is |x - y|.

Given the integer array position and the integer m. Return the required force.

Example 1:

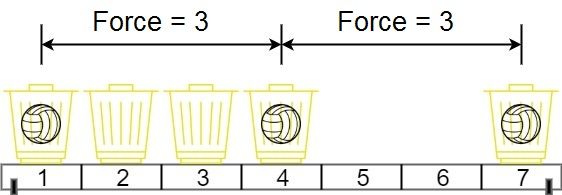
Input: position = [1,2,3,4,7], m = 3
Output: 3
Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.

Example 2:

Input: position = [5,4,3,2,1,1000000000], m = 2
Output: 999999999
Explanation: We can use baskets 1 and 1000000000.

Constraints:

n == position.length
2 <= n <= 10⁵
1 <= position[i] <= 10⁹
All integers in position are distinct.
2 <= m <= position.length

Solutions

Solution 1: Binary Search

We notice that the greater the minimum magnetic force between any two balls, the fewer balls can be placed, which exhibits monotonicity. We can use binary search to find the maximum minimum magnetic force that allows the number of balls not less than $m$ to be placed.

First, we sort the positions of the baskets, and then use binary search with the left boundary $l = 1$ and the right boundary $r = \textit{position}[n - 1]$, where $n$ is the number of baskets. In each binary search iteration, we calculate the midpoint $m = (l + r + 1) / 2$, and then determine if there is a way to place the balls such that the number of balls placed is not less than $m$.

The problem is transformed into determining whether a given minimum magnetic force $f$ can place $m$ balls. We can traverse the positions of the baskets from left to right, and if the distance between the position of the last ball and the current basket's position is greater than or equal to $f$, it indicates that a ball can be placed in the current basket. Finally, we check if the number of balls placed is not less than $m$.

The time complexity is $O(n \times \log n + n \times \log M)$, and the space complexity is $O(\log n)$. Here, $n$ and $M$ respectively represent the number of baskets and the maximum value of the basket positions.

Python3JavaC++GoTypeScriptJavaScript

class Solution:
    def maxDistance(self, position: List[int], m: int) -> int:
        def check(f: int) -> bool:
            prev = -inf
            cnt = 0
            for curr in position:
                if curr - prev >= f:
                    prev = curr
                    cnt += 1
            return cnt < m

        position.sort()
        l, r = 1, position[-1]
        return bisect_left(range(l, r + 1), True, key=check)

class Solution {
    private int[] position;

    public int maxDistance(int[] position, int m) {
        Arrays.sort(position);
        this.position = position;
        int l = 1, r = position[position.length - 1];
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (count(mid) >= m) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }

    private int count(int f) {
        int prev = position[0];
        int cnt = 1;
        for (int curr : position) {
            if (curr - prev >= f) {
                ++cnt;
                prev = curr;
            }
        }
        return cnt;
    }
}

class Solution {
public:
    int maxDistance(vector<int>& position, int m) {
        sort(position.begin(), position.end());
        int l = 1, r = position.back();
        auto count = [&](int f) {
            int prev = position[0];
            int cnt = 1;
            for (int& curr : position) {
                if (curr - prev >= f) {
                    prev = curr;
                    cnt++;
                }
            }
            return cnt;
        };
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (count(mid) >= m) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }
};

func maxDistance(position []int, m int) int {
    sort.Ints(position)
    return sort.Search(position[len(position)-1], func(f int) bool {
        prev := position[0]
        cnt := 1
        for _, curr := range position {
            if curr-prev >= f {
                cnt++
                prev = curr
            }
        }
        return cnt < m
    }) - 1
}

function maxDistance(position: number[], m: number): number {
    position.sort((a, b) => a - b);
    let [l, r] = [1, position.at(-1)!];
    const count = (f: number): number => {
        let cnt = 1;
        let prev = position[0];
        for (const curr of position) {
            if (curr - prev >= f) {
                cnt++;
                prev = curr;
            }
        }
        return cnt;
    };
    while (l < r) {
        const mid = (l + r + 1) >> 1;
        if (count(mid) >= m) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }
    return l;
}

/**
 * @param {number[]} position
 * @param {number} m
 * @return {number}
 */
var maxDistance = function (position, m) {
    position.sort((a, b) => a - b);
    let [l, r] = [1, position.at(-1)];
    const count = f => {
        let cnt = 1;
        let prev = position[0];
        for (const curr of position) {
            if (curr - prev >= f) {
                cnt++;
                prev = curr;
            }
        }
        return cnt;
    };
    while (l < r) {
        const mid = (l + r + 1) >> 1;
        if (count(mid) >= m) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }
    return l;
};

1552. Magnetic Force Between Two Balls

Description

Solutions

Solution 1: Binary Search

Comments