Skip to content

2103. Rings and Rods

Description

There are n rings and each ring is either red, green, or blue. The rings are distributed across ten rods labeled from 0 to 9.

You are given a string rings of length 2n that describes the n rings that are placed onto the rods. Every two characters in rings forms a color-position pair that is used to describe each ring where:

  • The first character of the ith pair denotes the ith ring's color ('R', 'G', 'B').
  • The second character of the ith pair denotes the rod that the ith ring is placed on ('0' to '9').

For example, "R3G2B1" describes n == 3 rings: a red ring placed onto the rod labeled 3, a green ring placed onto the rod labeled 2, and a blue ring placed onto the rod labeled 1.

Return the number of rods that have all three colors of rings on them.

 

Example 1:

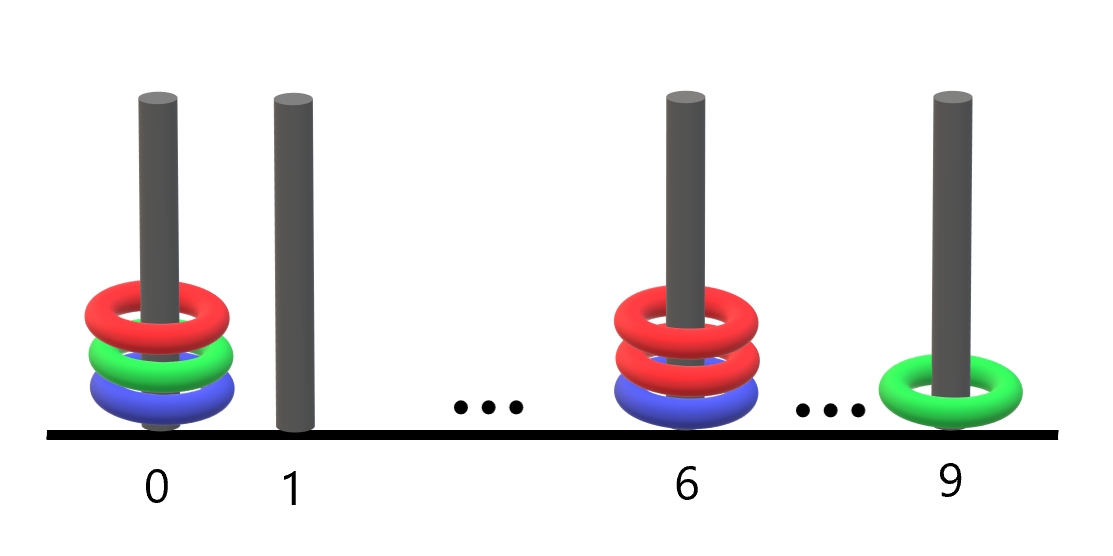
Input: rings = "B0B6G0R6R0R6G9"
Output: 1
Explanation: 
- The rod labeled 0 holds 3 rings with all colors: red, green, and blue.
- The rod labeled 6 holds 3 rings, but it only has red and blue.
- The rod labeled 9 holds only a green ring.
Thus, the number of rods with all three colors is 1.

Example 2:

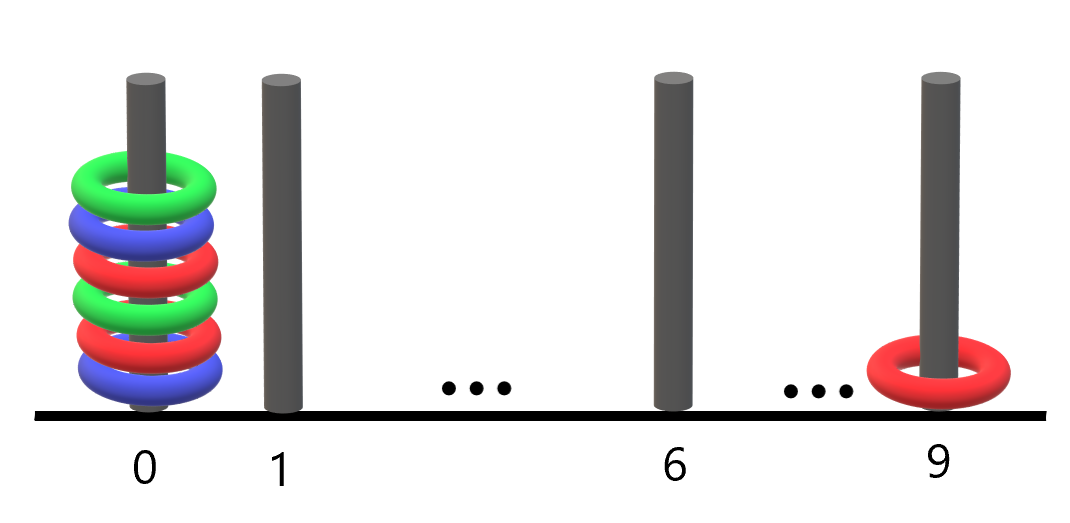
Input: rings = "B0R0G0R9R0B0G0"
Output: 1
Explanation: 
- The rod labeled 0 holds 6 rings with all colors: red, green, and blue.
- The rod labeled 9 holds only a red ring.
Thus, the number of rods with all three colors is 1.

Example 3:

Input: rings = "G4"
Output: 0
Explanation: 
Only one ring is given. Thus, no rods have all three colors.

 

Constraints:

  • rings.length == 2 * n
  • 1 <= n <= 100
  • rings[i] where i is even is either 'R', 'G', or 'B' (0-indexed).
  • rings[i] where i is odd is a digit from '0' to '9' (0-indexed).

Solutions

Solution 1: Bit Manipulation

We can use an array $mask$ of length $10$ to represent the color situation of the rings on each rod, where $mask[i]$ represents the color situation of the ring on the $i$th rod. If there are red, green, and blue rings on the $i$th rod, then the binary representation of $mask[i]$ is $111$, that is, $mask[i] = 7$.

We traverse the string $rings$. For each color position pair $(c, j)$, where $c$ represents the color of the ring and $j$ represents the number of the rod where the ring is located, we set the corresponding binary bit of $mask[j]$, that is, $mask[j] |= d[c]$, where $d[c]$ represents the binary bit corresponding to color $c$.

Finally, we count the number of elements in $mask$ that are $7$, which is the number of rods that have collected all three colors of rings.

The time complexity is $O(n)$, and the space complexity is $O(|\Sigma|)$, where $n$ represents the length of the string $rings$, and $|\Sigma|$ represents the size of the character set.

1
2
3
4
5
6
7
8
9
class Solution:
    def countPoints(self, rings: str) -> int:
        mask = [0] * 10
        d = {"R": 1, "G": 2, "B": 4}
        for i in range(0, len(rings), 2):
            c = rings[i]
            j = int(rings[i + 1])
            mask[j] |= d[c]
        return mask.count(7)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int countPoints(String rings) {
        int[] d = new int['Z'];
        d['R'] = 1;
        d['G'] = 2;
        d['B'] = 4;
        int[] mask = new int[10];
        for (int i = 0, n = rings.length(); i < n; i += 2) {
            int c = rings.charAt(i);
            int j = rings.charAt(i + 1) - '0';
            mask[j] |= d[c];
        }
        int ans = 0;
        for (int x : mask) {
            if (x == 7) {
                ++ans;
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution {
public:
    int countPoints(string rings) {
        int d['Z']{['R'] = 1, ['G'] = 2, ['B'] = 4};
        int mask[10]{};
        for (int i = 0, n = rings.size(); i < n; i += 2) {
            int c = rings[i];
            int j = rings[i + 1] - '0';
            mask[j] |= d[c];
        }
        return count(mask, mask + 10, 7);
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
func countPoints(rings string) (ans int) {
    d := ['Z']int{'R': 1, 'G': 2, 'B': 4}
    mask := [10]int{}
    for i, n := 0, len(rings); i < n; i += 2 {
        c := rings[i]
        j := int(rings[i+1] - '0')
        mask[j] |= d[c]
    }
    for _, x := range mask {
        if x == 7 {
            ans++
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
function countPoints(rings: string): number {
    const idx = (c: string) => c.charCodeAt