Skip to content

2374. Node With Highest Edge Score

Description

You are given a directed graph with n nodes labeled from 0 to n - 1, where each node has exactly one outgoing edge.

The graph is represented by a given 0-indexed integer array edges of length n, where edges[i] indicates that there is a directed edge from node i to node edges[i].

The edge score of a node i is defined as the sum of the labels of all the nodes that have an edge pointing to i.

Return the node with the highest edge score. If multiple nodes have the same edge score, return the node with the smallest index.

 

Example 1:

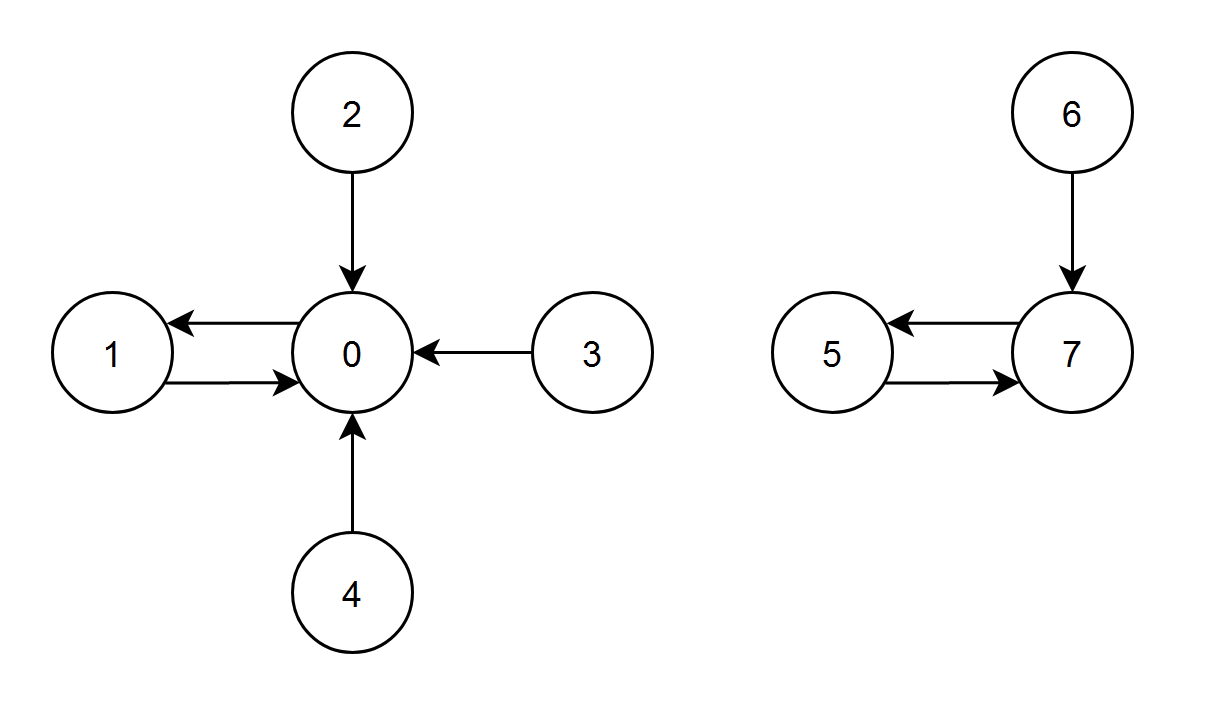
Input: edges = [1,0,0,0,0,7,7,5]
Output: 7
Explanation:
- The nodes 1, 2, 3 and 4 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 + 3 + 4 = 10.
- The node 0 has an edge pointing to node 1. The edge score of node 1 is 0.
- The node 7 has an edge pointing to node 5. The edge score of node 5 is 7.
- The nodes 5 and 6 have an edge pointing to node 7. The edge score of node 7 is 5 + 6 = 11.
Node 7 has the highest edge score so return 7.

Example 2:

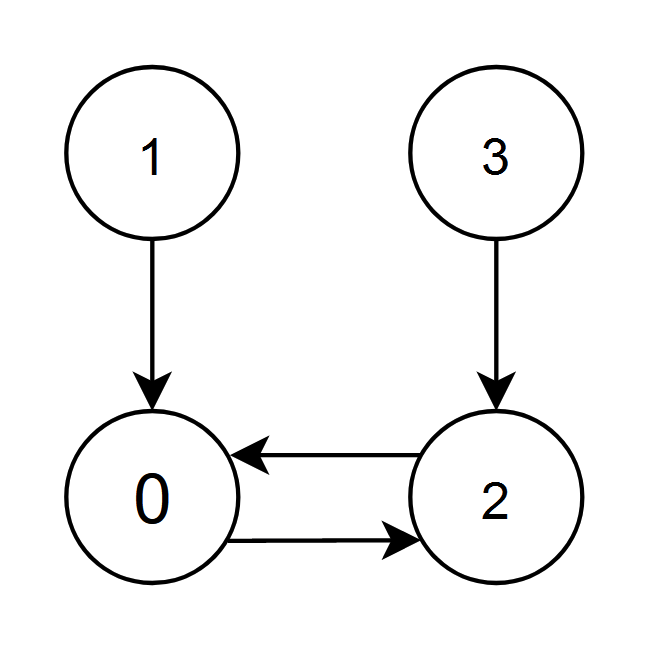
Input: edges = [2,0,0,2]
Output: 0
Explanation:
- The nodes 1 and 2 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 = 3.
- The nodes 0 and 3 have an edge pointing to node 2. The edge score of node 2 is 0 + 3 = 3.
Nodes 0 and 2 both have an edge score of 3. Since node 0 has a smaller index, we return 0.

 

Constraints:

  • n == edges.length
  • 2 <= n <= 105
  • 0 <= edges[i] < n
  • edges[i] != i

Solutions

Solution 1: Single Traversal

We define an array $\textit{cnt}$ of length $n$, where $\textit{cnt}[i]$ represents the edge score of node $i$. Initially, all elements are $0$. We also define an answer variable $\textit{ans}$, initially set to $0$.

Next, we traverse the array $\textit{edges}$. For each node $i$ and its outgoing edge node $j$, we update $\textit{cnt}[j]$ to $\textit{cnt}[j] + i$. If $\textit{cnt}[\textit{ans}] < \textit{cnt}[j]$ or $\textit{cnt}[\textit{ans}] = \textit{cnt}[j]$ and $j < \textit{ans}$, we update $\textit{ans}$ to $j$.

Finally, return $\textit{ans}$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the length of the array $\textit{edges}$.

1
2
3
4
5
6
7
8
9
class Solution:
    def edgeScore(self, edges: List[int]) -> int:
        ans = 0
        cnt = [0] * len(edges)
        for i, j in enumerate(edges):
            cnt[j] += i
            if cnt[ans] < cnt[j] or (cnt[ans] == cnt[j] and j < ans):
                ans = j
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
    public int edgeScore(int[] edges) {
        int n = edges.length;
        long[] cnt = new long[n];
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int j = edges[i];
            cnt[j] += i;
            if (cnt[ans] < cnt[j] || (cnt[ans] == cnt[j] && j < ans)) {
                ans = j;
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
public:
    int edgeScore(vector<int>& edges) {
        int n = edges.size();
        vector<long long> cnt(n);
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int j = edges[i];
            cnt[j] += i;
            if (cnt[ans] < cnt[j] || (cnt[ans] == cnt[j] && j < ans)) {
                ans = j;
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
func edgeScore(edges []int) (ans int) {
    cnt := make([]int, len(edges))
    for i, j := range edges {
        cnt[j] += i
        if cnt[ans] < cnt[j] || (cnt[ans] == cnt[j] && j < ans) {
            ans = j
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
function edgeScore(edges: number[]): number {
    const n = edges.length;
    const cnt: number[] = Array(n).fill(0);
    let ans: number = 0;
    for (let i = 0; i < n; ++i) {
        const j = edges[i];
        cnt[j] += i;
        if (cnt[ans] < cnt[j] || (cnt[ans] === cnt[j] && j < ans)) {
            ans = j;
        }
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
impl Solution {
    pub fn edge_score(edges: Vec<i32>) -> i32 {
        let n = edges.len();
        let mut cnt = vec![0_i64; n];
        let mut ans = 0;

        for (i, &j) in edges.iter().enumerate() {
            let j = j as usize;
            cnt[j] += i as i64;
            if cnt[ans] < cnt[j] || (cnt[ans] == cnt[j] && j < ans) {
                ans = j;
            }
        }

        ans as i32
    }
}

Comments