2002. Maximum Product of the Length of Two Palindromic Subsequences

Description

Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.

Return the maximum possible product of the lengths of the two palindromic subsequences.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.

 

Example 1:

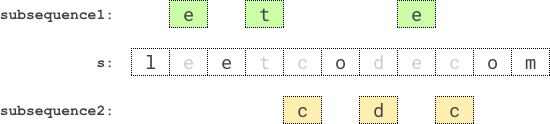
Input: s = "leetcodecom"
Output: 9
Explanation: An optimal solution is to choose "ete" for the 1st subsequence and "cdc" for the 2nd subsequence.
The product of their lengths is: 3 * 3 = 9.

Example 2:

Input: s = "bb"
Output: 1
Explanation: An optimal solution is to choose "b" (the first character) for the 1st subsequence and "b" (the second character) for the 2nd subsequence.
The product of their lengths is: 1 * 1 = 1.

Example 3:

Input: s = "accbcaxxcxx"
Output: 25
Explanation: An optimal solution is to choose "accca" for the 1st subsequence and "xxcxx" for the 2nd subsequence.
The product of their lengths is: 5 * 5 = 25.

 

Constraints:

• 2 <= s.length <= 12
• s consists of lowercase English letters only.

Solutions

Solution 1: Binary Enumeration

We notice that the length of the string \(s\) does not exceed \(12\), so we can use the method of binary enumeration to enumerate all subsequences of \(s\). Suppose the length of \(s\) is \(n\), we can use \(2^n\) binary numbers of length \(n\) to represent all subsequences of \(s\). For each binary number, the \(i\)-th bit being \(1\) means the \(i\)-th character of \(s\) is in the subsequence, and \(0\) means it is not in the subsequence. For each binary number, we judge whether it is a palindrome subsequence and record it in the array \(p\).

Next, we enumerate each number \(i\) in \(p\). If \(i\) is a palindrome subsequence, then we can enumerate a number \(j\) from the complement of \(i\), \(mx = (2^n - 1) \oplus i\). If \(j\) is also a palindrome subsequence, then \(i\) and \(j\) are the two palindrome subsequences we are looking for. Their lengths are the number of \(1\)s in the binary representation of \(i\) and \(j\), denoted as \(a\) and \(b\), respectively. Then their product is \(a \times b\). We take the maximum of all possible \(a \times b\).

The time complexity is \((2^n \times n + 3^n)\), and the space complexity is \(O(2^n)\). Here, \(n\) is the length of the string \(s\).

Python3JavaC++Go

class Solution:
    def maxProduct(self, s: str) -> int:
        n = len(s)
        p = [True] * (1 << n)
        for k in range(1, 1 << n):
            i, j = 0, n - 1
            while i < j:
                while i < j and (k >> i & 1) == 0:
                    i += 1
                while i < j and (k >> j & 1) == 0:
                    j -= 1
                if i < j and s[i] != s[j]:
                    p[k] = False
                    break
                i, j = i + 1, j - 1
        ans = 0
        for i in range(1, 1 << n):
            if p[i]:
                mx = ((1 << n) - 1) ^ i
                j = mx
                a = i.bit_count()
                while j:
                    if p[j]:
                        b = j.bit_count()
                        ans = max(ans, a * b)
                    j = (j - 1) & mx
        return ans

class Solution {
    public int maxProduct(String s) {
        int n = s.length();
        boolean[] p = new boolean[1 << n];
        Arrays.fill(p, true);
        for (int k = 1; k < 1 << n; ++k) {
            for (int i = 0, j = n - 1; i < n; ++i, --j) {
                while (i < j && (k >> i & 1) == 0) {
                    ++i;
                }
                while (i < j && (k >> j & 1) == 0) {
                    --j;
                }
                if (i < j && s.charAt(i) != s.charAt(j)) {
                    p[k] = false;
                    break;
                }
            }
        }
        int ans = 0;
        for (int i = 1; i < 1 << n; ++i) {
            if (p[i]) {
                int a = Integer.bitCount(i);
                int mx = ((1 << n) - 1) ^ i;
                for (int j = mx; j > 0; j = (j - 1) & mx) {
                    if (p[j]) {
                        int b = Integer.bitCount(j);
                        ans = Math.max(ans, a * b);
                    }
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    int maxProduct(string s) {
        int n = s.size();
        vector<bool> p(1 << n, true);
        for (int k = 1; k < 1 << n; ++k) {
            for (int i = 0, j = n - 1; i < j; ++i, --j) {
                while (i < j && !(k >> i & 1)) {
                    ++i;
                }
                while (i < j && !(k >> j & 1)) {
                    --j;
                }
                if (i < j && s[i] != s[j]) {
                    p[k] = false;
                    break;
                }
            }
        }
        int ans = 0;
        for (int i = 1; i < 1 << n; ++i) {
            if (p[i]) {
                int a = __builtin_popcount(i);
                int mx = ((1 << n) - 1) ^ i;
                for (int j = mx; j; j = (j - 1) & mx) {
                    if (p[j]) {
                        int b = __builtin_popcount(j);
                        ans = max(ans, a * b);
                    }
                }
            }
        }
        return ans;
    }
};

func maxProduct(s string) (ans int) {
    n := len(s)
    p := make([]bool, 1<<n)
    for i := range p {
        p[i] = true
    }
    for k := 1; k < 1<<n; k++ {
        for i, j := 0, n-1; i < j; i, j = i+1, j-1 {
            for i < j && (k>>i&1) == 0 {
                i++
            }
            for i < j && (k>>j&1) == 0 {
                j--
            }
            if i < j && s[i] != s[j] {
                p[k] = false
                break
            }
        }
    }
    for i := 1; i < 1<<n; i++ {
        if p[i] {
            a := bits.OnesCount(uint(i))
            mx := (1<<n - 1) ^ i
            for j := mx; j > 0; j = (j - 1) & mx {
                if p[j] {
                    b := bits.OnesCount(uint(j))
                    ans = max(ans, a*b)
                }
            }
        }
    }
    return

}

Comments