514. Freedom Trail

Description

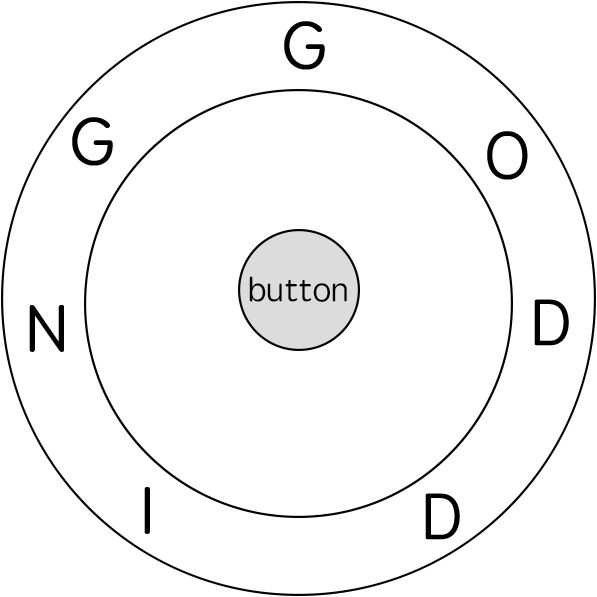
In the video game Fallout 4, the quest "Road to Freedom" requires players to reach a metal dial called the "Freedom Trail Ring" and use the dial to spell a specific keyword to open the door.

Given a string ring that represents the code engraved on the outer ring and another string key that represents the keyword that needs to be spelled, return the minimum number of steps to spell all the characters in the keyword.

Initially, the first character of the ring is aligned at the "12:00" direction. You should spell all the characters in key one by one by rotating ring clockwise or anticlockwise to make each character of the string key aligned at the "12:00" direction and then by pressing the center button.

At the stage of rotating the ring to spell the key character key[i]:

1. You can rotate the ring clockwise or anticlockwise by one place, which counts as one step. The final purpose of the rotation is to align one of ring's characters at the "12:00" direction, where this character must equal key[i].
2. If the character key[i] has been aligned at the "12:00" direction, press the center button to spell, which also counts as one step. After the pressing, you could begin to spell the next character in the key (next stage). Otherwise, you have finished all the spelling.

 

Example 1:

Input: ring = "godding", key = "gd"
Output: 4
Explanation:
For the first key character 'g', since it is already in place, we just need 1 step to spell this character. 
For the second key character 'd', we need to rotate the ring "godding" anticlockwise by two steps to make it become "ddinggo".
Also, we need 1 more step for spelling.
So the final output is 4.

Example 2:

Input: ring = "godding", key = "godding"
Output: 13

 

Constraints:

• 1 <= ring.length, key.length <= 100
• ring and key consist of only lower case English letters.
• It is guaranteed that key could always be spelled by rotating ring.

Solutions

Solution 1: Dynamic Programming

First, we preprocess the positions of each character $c$ in the string $ring$, and record them in the array $pos[c]$. Suppose the lengths of the strings $key$ and $ring$ are $m$ and $n$, respectively.

Then we define $f[i][j]$ as the minimum number of steps to spell the first $i+1$ characters of the string $key$, and the $j$-th character of $ring$ is aligned with the $12:00$ direction. Initially, $f[i][j]=+\infty$. The answer is $\min_{0 \leq j < n} f[m - 1][j]$.

We can first initialize $f[0][j]$, where $j$ is the position where the character $key[0]$ appears in $ring$. Since the $j$-th character of $ring$ is aligned with the $12:00$ direction, we only need $1$ step to spell $key[0]$. In addition, we need $min(j, n - j)$ steps to rotate $ring$ to the $12:00$ direction. Therefore, $f[0][j]=min(j, n - j) + 1$.

Next, we consider how the state transitions when $i \geq 1$. We can enumerate the position list $pos[key[i]]$ where $key[i]$ appears in $ring$, and enumerate the position list $pos[key[i-1]]$ where $key[i-1]$ appears in $ring$, and then update $f[i][j]$, i.e., $f[i][j]=\min_{k \in pos[key[i-1]]} f[i-1][k] + \min(\textit{abs}(j - k), n - \textit{abs}(j - k)) + 1$.

Finally, we return $\min_{0 \leq j \lt n} f[m - 1][j]$.

The time complexity is $O(m \times n^2)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the lengths of the strings $key$ and $ring$, respectively.

Python3JavaC++GoTypeScript

class Solution:
    def findRotateSteps(self, ring: str, key: str) -> int:
        m, n = len(key), len(ring)
        pos = defaultdict(list)
        for i, c in enumerate(ring):
            pos[c].append(i)
        f = [[inf] * n for _ in range(m)]
        for j in pos[key[0]]:
            f[0][j] = min(j, n - j) + 1
        for i in range(1, m):
            for j in pos[key[i]]:
                for k in pos[key[i - 1]]:
                    f[i][j] = min(
                        f[i][j], f[i - 1][k] + min(abs(j - k), n - abs(j - k)) + 1
                    )
        return min(f[-1][j] for j in pos[key[-1]])

class Solution {
    public int findRotateSteps(String ring, String key) {
        int m = key.length(), n = ring.length();
        List<Integer>[] pos = new List[26];
        Arrays.setAll(pos, k -> new ArrayList<>());
        for (int i = 0; i < n; ++i) {
            int j = ring.charAt(i) - 'a';
            pos[j].add(i);
        }
        int[][] f = new int[m][n];
        for (var g : f) {
            Arrays.fill(g, 1 << 30);
        }
        for (int j : pos[key.charAt(0) - 'a']) {
            f[0][j] = Math.min(j, n - j) + 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j : pos[key.charAt(i) - 'a']) {
                for (int k : pos[key.charAt(i - 1) - 'a']) {
                    f[i][j] = Math.min(
                        f[i][j], f[i - 1][k] + Math.min(Math.abs(j - k), n - Math.abs(j - k)) + 1);
                }
            }
        }
        int ans = 1 << 30;
        for (int j : pos[key.charAt(m - 1) - 'a']) {
            ans = Math.min(ans, f[m - 1][j]);
        }
        return ans;
    }
}

class Solution {
public:
    int findRotateSteps(string ring, string key) {
        int m = key.size(), n = ring.size();
        vector<int> pos[26];
        for (int j = 0; j < n; ++j) {
            pos[ring[j] - 'a'].push_back(j);
        }
        int f[m][n];
        memset(f, 0x3f, sizeof(f));
        for (int j : pos[key[0] - 'a']) {
            f[0][j] = min(j, n - j) + 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j : pos[key[i] - 'a']) {
                for (int k : pos[key[i - 1] - 'a']) {
                    f[i][j] = min(f[i][j], f[i - 1][k] + min(abs(j - k), n - abs(j - k)) + 1);
                }
            }
        }
        int ans = 1 << 30;
        for (int j : pos[key[m - 1] - 'a']) {
            ans = min(ans, f[m - 1][j]);
        }
        return ans;
    }
};

func findRotateSteps(ring string, key string) int {
    m, n := len(key), len(ring)
    pos := [26][]int{}
    for j, c := range ring {
        pos[c-'a'] = append(pos[c-'a'], j)
    }
    f := make([][]int, m)
    for i := range f {
        f[i] = make([]int, n)
        for j := range f[i] {
            f[i][j] = 1 << 30
        }
    }
    for _, j := range pos[key[0]-'a'] {
        f[0][j] = min(j, n-j) + 1
    }
    for i := 1; i < m; i++ {
        for _, j := range pos[key[i]-'a'] {
            for _, k := range pos[key[i-1]-'a'] {
                f[i][j] = min(f[i][j], f[i-1][k]+min(abs(j-k), n-abs(j-k))+1)
            }
        }
    }
    ans := 1 << 30
    for _, j := range pos[key[m-1]-'a'] {
        ans = min(ans, f[m-1][j])
    }
    return ans
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

function findRotateSteps(ring: string, key: string): number {
    const m: number = key.length;
    const n: number = ring.length;
    const pos: number[][] = Array.from({ length: 26 }, () => []);
    for (let i = 0; i < n; ++i) {
        const j: number = ring.charCodeAt(i) - 'a'.charCodeAt(0);
        pos[j].push(i);
    }

    const f: number[][] = Array.from({ length: m }, () => Array(n).fill(1 << 30));
    for (const j of pos[key.charCodeAt(0) - 'a'.charCodeAt(0)]) {
        f[0][j] = Math.min(j, n - j) + 1;
    }

    for (let i = 1; i < m; ++i) {
        for (const j of pos[key.charCodeAt(i) - 'a'.charCodeAt(0)]) {
            for (const k of pos[key.charCodeAt(i - 1) - 'a'.charCodeAt(0)]) {
                f[i][j] = Math.min(
                    f[i][j],
                    f[i - 1][k] + Math.min(Math.abs(j - k), n - Math.abs(j - k)) + 1,
                );
            }
        }
    }

    let ans: number = 1 << 30;
    for (const j of pos[key.charCodeAt(m - 1) - 'a'.charCodeAt(0)]) {
        ans = Math.min(ans, f[m - 1][j]);
    }
    return ans;
}

Comments