Depth-First Search
Breadth-First Search
Graph
Shortest Path
Heap (Priority Queue)
Description
You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui , vi , wi ), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target.
We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal . If it is impossible for all the n nodes to receive the signal, return -1.
Example 1:
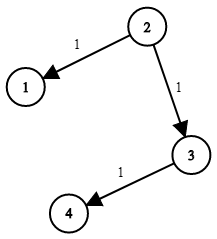
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2
Example 2:
Input: times = [[1,2,1]], n = 2, k = 1
Output: 1
Example 3:
Input: times = [[1,2,1]], n = 2, k = 2
Output: -1
Constraints:
1 <= k <= n <= 1001 <= times.length <= 6000times[i].length == 31 <= ui , vi <= nui != vi 0 <= wi <= 100All the pairs (ui , vi ) are unique . (i.e., no multiple edges.)
Solutions
Solution 1
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 class Solution :
def networkDelayTime ( self , times : List [ List [ int ]], n : int , k : int ) -> int :
INF = 0x3F3F
dist = [ INF ] * n
vis = [ False ] * n
g = [[ INF ] * n for _ in range ( n )]
for u , v , w in times :
g [ u - 1 ][ v - 1 ] = w
dist [ k - 1 ] = 0
for _ in range ( n ):
t = - 1
for j in range ( n ):
if not vis [ j ] and ( t == - 1 or dist [ t ] > dist [ j ]):
t = j
vis [ t ] = True
for j in range ( n ):
dist [ j ] = min ( dist [ j ], dist [ t ] + g [ t ][ j ])
ans = max ( dist )
return - 1 if ans == INF else ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 class Solution {
private static final int INF = 0x3f3f ;
public int networkDelayTime ( int [][] times , int n , int k ) {
int [][] g = new int [ n ][ n ] ;
int [] dist = new int [ n ] ;
boolean [] vis = new boolean [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
dist [ i ] = INF ;
Arrays . fill ( g [ i ] , INF );
}
for ( int [] t : times ) {
g [ t [ 0 ] - 1 ][ t [ 1 ] - 1 ] = t [ 2 ] ;
}
dist [ k - 1 ] = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
int t = - 1 ;
for ( int j = 0 ; j < n ; ++ j ) {
if ( ! vis [ j ] && ( t == - 1 || dist [ t ] > dist [ j ] )) {
t = j ;
}
}
vis [ t ] = true ;
for ( int j = 0 ; j < n ; ++ j ) {
dist [ j ] = Math . min ( dist [ j ] , dist [ t ] + g [ t ][ j ] );
}
}
int ans = 0 ;
for ( int d : dist ) {
ans = Math . max ( ans , d );
}
return ans == INF ? - 1 : ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 class Solution {
public :
const int inf = 0x3f3f ;
int networkDelayTime ( vector < vector < int >>& times , int n , int k ) {
vector < vector < int >> g ( n , vector < int > ( n , inf ));
for ( auto & t : times ) g [ t [ 0 ] - 1 ][ t [ 1 ] - 1 ] = t [ 2 ];
vector < bool > vis ( n );
vector < int > dist ( n , inf );
dist [ k - 1 ] = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
int t = -1 ;
for ( int j = 0 ; j < n ; ++ j ) {
if ( ! vis [ j ] && ( t == -1 || dist [ t ] > dist [ j ])) {
t = j ;
}
}
vis [ t ] = true ;
for ( int j = 0 ; j < n ; ++ j ) {
dist [ j ] = min ( dist [ j ], dist [ t ] + g [ t ][ j ]);
}
}
int ans = * max_element ( dist . begin (), dist . end ());
return ans == inf ? -1 : ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 func networkDelayTime ( times [][] int , n int , k int ) int {
const inf = 0x3f3f
dist := make ([] int , n )
vis := make ([] bool , n )
g := make ([][] int , n )
for i := range dist {
dist [ i ] = inf
g [ i ] = make ([] int , n )
for j := range g [ i ] {
g [ i ][ j ] = inf
}
}
for _ , t := range times {
g [ t [ 0 ] - 1 ][ t [ 1 ] - 1 ] = t [ 2 ]
}
dist [ k - 1 ] = 0
for i := 0 ; i < n ; i ++ {
t := - 1
for j := 0 ; j < n ; j ++ {
if ! vis [ j ] && ( t == - 1 || dist [ t ] > dist [ j ]) {
t = j
}
}
vis [ t ] = true
for j := 0 ; j < n ; j ++ {
dist [ j ] = min ( dist [ j ], dist [ t ] + g [ t ][ j ])
}
}
ans := slices . Max ( dist )
if ans == inf {
return - 1
}
return ans
}
Solution 2
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 class Solution :
def networkDelayTime ( self , times : List [ List [ int ]], n : int , k : int ) -> int :
INF = 0x3F3F
g = defaultdict ( list )
for u , v , w in times :
g [ u - 1 ] . append (( v - 1 , w ))
dist = [ INF ] * n
dist [ k - 1 ] = 0
q = [( 0 , k - 1 )]
while q :
_ , u = heappop ( q )
for v , w in g [ u ]:
if dist [ v ] > dist [ u ] + w :
dist [ v ] = dist [ u ] + w
heappush ( q , ( dist [ v ], v ))
ans = max ( dist )
return - 1 if ans == INF else ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 class Solution {
private static final int INF = 0x3f3f ;
public int networkDelayTime ( int [][] times , int n , int k ) {
List < int []>[] g = new List [ n ] ;
int [] dist = new int [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
dist [ i ] = INF ;
g [ i ] = new ArrayList <> ();
}
for ( int [] t : times ) {
g [ t [ 0 ] - 1 ] . add ( new int [] { t [ 1 ] - 1 , t [ 2 ] });
}
dist [ k - 1 ] = 0 ;
PriorityQueue < int []> q = new PriorityQueue <> ( Comparator . comparingInt ( a -> a [ 0 ] ));
q . offer ( new int [] { 0 , k - 1 });
while ( ! q . isEmpty ()) {
int [] p = q . poll ();
int u = p [ 1 ] ;
for ( int [] ne : g [ u ] ) {
int v = ne [ 0 ] , w = ne [ 1 ] ;
if ( dist [ v ] > dist [ u ] + w ) {
dist [ v ] = dist [ u ] + w ;
q . offer ( new int [] { dist [ v ] , v });
}
}
}
int ans = 0 ;
for ( int d : dist ) {
ans = Math . max ( ans , d );
}
return ans == INF ? - 1 : ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 class Solution {
public :
const int inf = 0x3f3f ;
int networkDelayTime ( vector < vector < int >>& times , int n , int k ) {
vector < vector < vector < int >>> g ( n );
for ( auto & t : times ) g [ t [ 0 ] - 1 ]. push_back ({ t [ 1 ] - 1 , t [ 2 ]});
vector < int > dist ( n , inf );
dist [ k - 1 ] = 0 ;
priority_queue < vector < int > , vector < vector < int >> , greater < vector < int >>> q ;
q . push ({ 0 , k - 1 });
while ( ! q . empty ()) {
auto p = q . top ();
q . pop ();
int u = p [ 1 ];
for ( auto & ne : g [ u ]) {
int v = ne [ 0 ], w = ne [ 1 ];
if ( dist [ v ] > dist [ u ] + w ) {
dist [ v ] = dist [ u ] + w ;
q . push ({ dist [ v ], v });
}
}
}
int ans = * max_element ( dist . begin (), dist . end ());
return ans == inf ? -1 : ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 const Inf = 0x3f3f3f3f
type pair struct {
first int
second int
}
var _ heap . Interface = ( * pairs )( nil )
type pairs [] pair
func ( a pairs ) Len () int { return len ( a ) }
func ( a pairs ) Less ( i int , j int ) bool {
return a [ i ]. first < a [ j ]. first || a [ i ]. first == a [ j ]. first && a [ i ]. second < a [ j ]. second
}
func ( a pairs ) Swap ( i int , j int ) { a [ i ], a [ j ] = a [ j ], a [ i ] }
func ( a * pairs ) Push ( x any ) { * a = append ( * a , x .( pair )) }
func ( a * pairs ) Pop () any { l := len ( * a ); t := ( * a )[ l - 1 ]; * a = ( * a )[: l - 1 ]; return t }
func networkDelayTime ( times [][] int , n int , k int ) int {
graph := make ([] pairs , n )
for _ , time := range times {
from , to , time := time [ 0 ] - 1 , time [ 1 ] - 1 , time [ 2 ]
graph [ from ] = append ( graph [ from ], pair { to , time })
}
dis := make ([] int , n )
for i := range dis {
dis [ i ] = Inf
}
dis [ k - 1 ] = 0
vis := make ([] bool , n )
h := make ( pairs , 0 )
heap . Push ( & h , pair { 0 , k - 1 })
for len ( h ) > 0 {
from := heap . Pop ( & h ).( pair ). second
if vis [ from ] {
continue
}
vis [ from ] = true
for _ , e := range graph [ from ] {
to , d := e . first , dis [ from ] + e . second
if d < dis [ to ] {
dis [ to ] = d
heap . Push ( & h , pair { d , to })
}
}
}
ans := slices . Max ( dis )
if ans == Inf {
return - 1
}
return ans
}
Solution 3
Python3 Java C++ Go
class Solution :
def networkDelayTime ( self , times : List [ List [ int ]], n : int , k : int ) -> int :
INF = 0x3F3F
dist = [ INF ] * n
dist [ k - 1 ] = 0
for _ in range ( n ):
backup = dist [:]
for u , v , w in times :
dist [ v - 1 ] = min ( dist [ v - 1 ], dist [ u - 1 ] + w )
ans = max ( dist )
return - 1 if ans == INF else ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 class Solution {
private static final int INF = 0x3f3f ;
public int networkDelayTime ( int [][] times , int n , int k ) {
int [] dist = new int [ n ] ;
int [] backup = new int [ n ] ;
Arrays . fill ( dist , INF );
dist [ k - 1 ] = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
System . arraycopy ( dist , 0 , backup , 0 , n );
for ( int [] t : times ) {
int u = t [ 0 ] - 1 , v = t [ 1 ] - 1 , w = t [ 2 ] ;
dist [ v ] = Math . min ( dist [ v ] , backup [ u ] + w );
}
}
int ans = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
ans = Math . max ( ans , dist [ i ] );
}
return ans == INF ? - 1 : ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 class Solution {
public :
int inf = 0x3f3f ;
int networkDelayTime ( vector < vector < int >>& times , int n , int k ) {
vector < int > dist ( n , inf );
dist [ k - 1 ] = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
vector < int > backup = dist ;
for ( auto & e : times ) {
int u = e [ 0 ] - 1 , v = e [ 1 ] - 1 , w = e [ 2 ];
dist [ v ] = min ( dist [ v ], backup [ u ] + w );
}
}
int ans = * max_element ( dist . begin (), dist . end ());
return ans == inf ? -1 : ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 func networkDelayTime ( times [][] int , n int , k int ) int {
const inf = 0x3f3f
dist := make ([] int , n )
backup := make ([] int , n )
for i := range dist {
dist [ i ] = inf
}
dist [ k - 1 ] = 0
for i := 0 ; i < n ; i ++ {
copy ( backup , dist )
for _ , e := range times {
u , v , w := e [ 0 ] - 1 , e [ 1 ] - 1 , e [ 2 ]
dist [ v ] = min ( dist [ v ], backup [ u ] + w )
}
}
ans := slices . Max ( dist )
if ans == inf {
return - 1
}
return ans
}
Solution 4
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 class Solution :
def networkDelayTime ( self , times : List [ List [ int ]], n : int , k : int ) -> int :
INF = 0x3F3F
dist = [ INF ] * n
vis = [ False ] * n
g = defaultdict ( list )
for u , v , w in times :
g [ u - 1 ] . append (( v - 1 , w ))
k -= 1
dist [ k ] = 0
q = deque ([ k ])
vis [ k ] = True
while q :
u = q . popleft ()
vis [ u ] = False
for v , w in g [ u ]:
if dist [ v ] > dist [ u ] + w :
dist [ v ] = dist [ u ] + w
if not vis [ v ]:
q . append ( v )
vis [ v ] = True
ans = max ( dist )
return - 1 if ans == INF else ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 class Solution {
private static final int INF = 0x3f3f ;
public int networkDelayTime ( int [][] times , int n , int k ) {
int [] dist = new int [ n ] ;
boolean [] vis = new boolean [ n ] ;
List < int []>[] g = new List [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
dist [ i ] = INF ;
g [ i ] = new ArrayList <> ();
}
for ( int [] t : times ) {
int u = t [ 0 ] - 1 , v = t [ 1 ] - 1 , w = t [ 2 ] ;
g [ u ] . add ( new int [] { v , w });
}
-- k ;
dist [ k ] = 0 ;
Deque < Integer > q = new ArrayDeque <> ();
q . offer ( k );
vis [ k ] = true ;
while ( ! q . isEmpty ()) {
int u = q . poll ();
vis [ u ] = false ;
for ( int [] ne : g [ u ] ) {
int v = ne [ 0 ] , w = ne [ 1 ] ;
if ( dist [ v ] > dist [ u ] + w ) {
dist [ v ] = dist [ u ] + w ;
if ( ! vis [ v ] ) {
q . offer ( v );
vis [ v ] = true ;
}
}
}
}
int ans = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
ans = Math . max ( ans , dist [ i ] );
}
return ans == INF ? - 1 : ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 class Solution {
public :
const int inf = 0x3f3f ;
int networkDelayTime ( vector < vector < int >>& times , int n , int k ) {
vector < int > dist ( n , inf );
vector < vector < vector < int >>> g ( n );
for ( auto & e : times ) {
int u = e [ 0 ] - 1 , v = e [ 1 ] - 1 , w = e [ 2 ];
g [ u ]. push_back ({ v , w });
}
vector < bool > vis ( n );
-- k ;
queue < int > q {{ k }};
vis [ k ] = true ;
dist [ k ] = 0 ;
while ( ! q . empty ()) {
int u = q . front ();
q . pop ();
vis [ u ] = false ;
for ( auto & ne : g [ u ]) {
int v = ne [ 0 ], w = ne [ 1 ];
if ( dist [ v ] > dist [ u ] + w ) {
dist [ v ] = dist [ u ] + w ;
if ( ! vis [ v ]) {
q . push ( v );
vis [ v ] = true ;
}
}
}
}
int ans = * max_element ( dist . begin (), dist . end ());
return ans == inf ? -1 : ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 func networkDelayTime ( times [][] int , n int , k int ) int {
const inf = 0x3f3f
dist := make ([] int , n )
vis := make ([] bool , n )
g := make ([][][] int , n )
for i := range dist {
dist [ i ] = inf
}
for _ , t := range times {
u , v , w := t [ 0 ] - 1 , t [ 1 ] - 1 , t [ 2 ]
g [ u ] = append ( g [ u ], [] int { v , w })
}
k --
dist [ k ] = 0
q := [] int { k }
vis [ k ] = true
for len ( q ) > 0 {
u := q [ 0 ]
q = q [ 1 :]
vis [ u ] = false
for _ , ne := range g [ u ] {
v , w := ne [ 0 ], ne [ 1 ]
if dist [ v ] > dist [ u ] + w {
dist [ v ] = dist [ u ] + w
if ! vis [ v ] {
q = append ( q , v )
vis [ v ] = true
}
}
}
}
ans := slices . Max ( dist )
if ans == inf {
return - 1
}
return ans
}
GitHub