Skip to content

1786. Number of Restricted Paths From First to Last Node

Description

There is an undirected weighted connected graph. You are given a positive integer n which denotes that the graph has n nodes labeled from 1 to n, and an array edges where each edges[i] = [ui, vi, weighti] denotes that there is an edge between nodes ui and vi with weight equal to weighti.

A path from node start to node end is a sequence of nodes [z0, z1, z2, ..., zk] such that z0 = start and zk = end and there is an edge between zi and zi+1 where 0 <= i <= k-1.

The distance of a path is the sum of the weights on the edges of the path. Let distanceToLastNode(x) denote the shortest distance of a path between node n and node x. A restricted path is a path that also satisfies that distanceToLastNode(zi) > distanceToLastNode(zi+1) where 0 <= i <= k-1.

Return the number of restricted paths from node 1 to node n. Since that number may be too large, return it modulo 109 + 7.

 

Example 1:

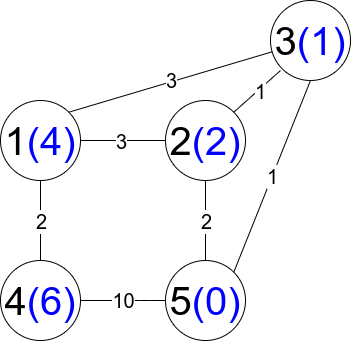
Input: n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
Output: 3
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The three restricted paths are:
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

Example 2:

Input: n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
Output: 1
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The only restricted path is 1 --> 3 --> 7.

 

Constraints:

  • 1 <= n <= 2 * 104
  • n - 1 <= edges.length <= 4 * 104
  • edges[i].length == 3
  • 1 <= ui, vi <= n
  • ui != vi
  • 1 <= weighti <= 105
  • There is at most one edge between any two nodes.
  • There is at least one path between any two nodes.

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def countRestrictedPaths(self, n: int, edges: List[List[int]]) -> int:
        @cache
        def dfs(i):
            if i == n:
                return 1
            ans = 0
            for j, _ in g[i]:
                if dist[i] > dist[j]:
                    ans = (ans + dfs(j)) % mod
            return ans

        g = defaultdict(list)
        for u, v, w in edges:
            g[u].append((v, w))
            g[v].append((u, w))
        q = [(0, n)]
        dist = [inf] * (n + 1)
        dist[n] = 0
        mod = 10**9 + 7
        while q:
            _, u = heappop(q)
            for v, w in g[u]:
                if dist[v] > dist[u] + w:
                    dist[v] = dist[u] + w
                    heappush(q, (dist[v], v))
        return dfs(1)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Solution {
    private static final int INF = Integer.MAX_VALUE;
    private static final int MOD = (int) 1e9 + 7;
    private List<int[]>[] g;
    private int[] dist;
    private int[] f;
    private int n;

    public int countRestrictedPaths(int n, int[][] edges) {
        this.n = n;
        g = new List[n + 1];
        for (int i = 0; i < g.length; ++i) {
            g[i] = new ArrayList<>();
        }
        for (int[] e : edges) {
            int u = e[0], v = e[1], w = e[2];
            g[u].add(new int[] {v, w});
            g[v].add(new int[] {u, w});
        }
        PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        q.offer(new int[] {0, n});
        dist = new int[n + 1];
        f = new int[n + 1];
        Arrays.fill(dist, INF);
        Arrays.fill(f, -1);
        dist[n] = 0;
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int u = p[1];
            for (int[] ne : g[u]) {
                int v = ne[0], w = ne[1];
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;