2608. Shortest Cycle in a Graph

Description

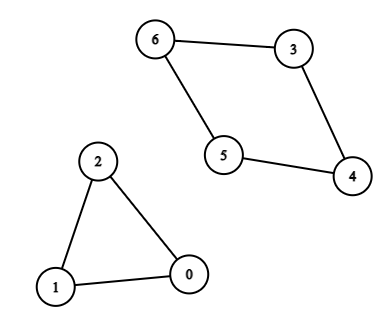
There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1. The edges in the graph are represented by a given 2D integer array edges, where edges[i] = [u_i, v_i] denotes an edge between vertex u_i and vertex v_i. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

Return the length of the shortest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.

Example 1:

Input: n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
Output: 3
Explanation: The cycle with the smallest length is : 0 -> 1 -> 2 -> 0

Example 2:

Input: n = 4, edges = [[0,1],[0,2]]
Output: -1
Explanation: There are no cycles in this graph.

Constraints:

2 <= n <= 1000
1 <= edges.length <= 1000
edges[i].length == 2
0 <= u_i, v_i < n
u_i != v_i
There are no repeated edges.

Solutions

Solution 1: Enumerate edges + BFS

We first construct the adjacency list $g$ of the graph according to the array $edges$, where $g[u]$ represents all the adjacent vertices of vertex $u$.

Then we enumerate the two-directional edge $(u, v)$, if the path from vertex $u$ to vertex $v$ still exists after deleting this edge, then the length of the shortest cycle containing this edge is $dist[v] + 1$, where $dist[v]$ represents the shortest path length from vertex $u$ to vertex $v$. We take the minimum of all these cycles.

The time complexity is $O(m^2)$ and the space complexity is $O(m + n)$, where $m$ and $n$ are the length of the array $edges$ and the number of vertices.

Python3JavaC++GoTypeScript

class Solution:
    def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:
        def bfs(u: int, v: int) -> int:
            dist = [inf] * n
            dist[u] = 0
            q = deque([u])
            while q:
                i = q.popleft()
                for j in g[i]:
                    if (i, j) != (u, v) and (j, i) != (u, v) and dist[j] == inf:
                        dist[j] = dist[i] + 1
                        q.append(j)
            return dist[v] + 1

        g = defaultdict(set)
        for u, v in edges:
            g[u].add(v)
            g[v].add(u)
        ans = min(bfs(u, v) for u, v in edges)
        return ans if ans < inf else -1

class Solution {
    private List<Integer>[] g;
    private final int inf = 1 << 30;

    public int findShortestCycle(int n, int[][] edges) {
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int u = e[0], v = e[1];
            g[u].add(v);
            g[v].add(u);
        }
        int ans = inf;
        for (var e : edges) {
            int u = e[0], v = e[1];
            ans = Math.min(ans, bfs(u, v));
        }
        return ans < inf ? ans : -1;
    }

    private int bfs(int u, int v) {
        int[] dist = new int[g.length];
        Arrays.fill(dist, inf);
        dist[u] = 0;
        Deque<Integer> q = new ArrayDeque<>();
        q.offer(u);
        while (!q.isEmpty()) {
            int i = q.poll();
            for (int j : g[i]) {
                if ((i == u && j == v) || (i == v && j == u) || dist[j] != inf) {
                    continue;
                }
                dist[j] = dist[i] + 1;
                q.offer(j);
            }
        }
        return dist[v] + 1;
    }
}

class Solution {
public:
    int findShortestCycle(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            int u = e[0], v = e[1];
            g[u].push_back(v);
            g[v].push_back(u);
        }
        const int inf = 1 << 30;
        auto bfs = [&](int u, int v) -> int {
            int dist[n];
            fill(dist, dist + n, inf);
            dist[u] = 0;
            queue<int> q{{u}};
            while (!q.empty()) {
                int i = q.front();
                q.pop();
                for (int j : g[i]) {
                    if ((i == u && j == v) || (i == v && j == u) || dist[j] != inf) {
                        continue;
                    }
                    dist[j] = dist[i] + 1;
                    q.push(j);
                }
            }
            return dist[v] + 1;
        };
        int ans = inf;
        for (auto& e : edges) {
            int u = e[0], v = e[1];
            ans = min(ans, bfs(u, v));
        }
        return ans < inf ? ans : -1;
    }
};

func findShortestCycle(n int, edges [][]int) int {
    g := make([][]int, n)
    for _, e := range edges {
        u, v := e[0], e[1]
        g[u] = append(g[u], v)
        g[v] = append(g[v], u)
    }
    const inf = 1 << 30
    bfs := func(u, v int) int {
        dist := make([]int, n)
        for i := range dist {
            dist[i] = inf
        }
        dist[u] = 0
        q := []int{u}
        for len(q) > 0 {
            i := q[0]
            q = q[1:]
            for _, j := range g[i] {
                if (i == u && j == v) || (i == v && j == u) || dist[j] != inf {
                    continue
                }
                dist[j] = dist[i] + 1
                q = append(q, j)
            }
        }
        return dist[v] + 1
    }
    ans := inf
    for _, e := range edges {
        u, v := e[0], e[1]
        ans = min(ans, bfs(u, v))
    }
    if ans < inf {
        return ans
    }
    return -1
}

function findShortestCycle(n: number, edges: number[][]): number {
    const g: number[][] = new Array(n).fill(0).map(() => []);
    for (const [u, v] of edges) {
        g[u].push(v);
        g[v].push(u);
    }
    const inf = 1 << 30;
    let ans = inf;
    const bfs = (u: number, v: number) => {
        const dist: number[] = new Array(n).fill(inf);
        dist[u] = 0;
        const q: number[] = [u];
        while (q.length) {
            const i = q.shift()!;
            for (const j of g[i]) {
                if ((i == u && j == v) || (i == v && j == u) || dist[j] != inf) {
                    continue;
                }
                dist[j] = dist[i] + 1;
                q.push(j);
            }
        }
        return 1 + dist[v];
    };
    for (const [u, v] of edges) {
        ans = Math.min(ans, bfs(u, v));
    }
    return ans < inf ? ans : -1;
}

Solution 2: Enumerate points + BFS

Similar to Solution 1, we first construct the adjacency list $g$ of the graph according to the array $edges$, where $g[u]$ represents all the adjacent vertices of vertex $u$.

Then we enumerate the vertex $u$, if there are two paths from vertex $u$ to vertex $v$, then we currently find a cycle, the length is the sum of the length of the two paths. We take the minimum of all these cycles.

The time complexity is $O(m \times n)$ and the space complexity is $O(m + n)$, where $m$ and $n$ are the length of the array $edges$ and the number of vertices.