2440. Create Components With Same Value

Description

There is an undirected tree with n nodes labeled from 0 to n - 1.

You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the ith node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

You are allowed to delete some edges, splitting the tree into multiple connected components. Let the value of a component be the sum of all nums[i] for which node i is in the component.

Return the maximum number of edges you can delete, such that every connected component in the tree has the same value.

 

Example 1:

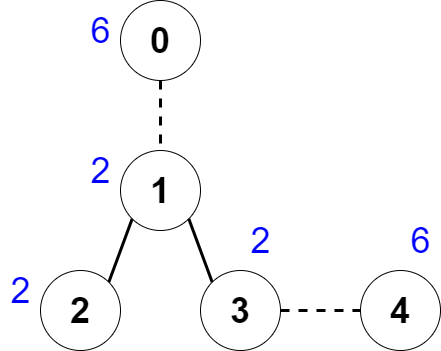
Input: nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]] 
Output: 2 
Explanation: The above figure shows how we can delete the edges [0,1] and [3,4]. The created components are nodes [0], [1,2,3] and [4]. The sum of the values in each component equals 6. It can be proven that no better deletion exists, so the answer is 2.

Example 2:

Input: nums = [2], edges = []
Output: 0
Explanation: There are no edges to be deleted.

 

Constraints:

• 1 <= n <= 2 * 104
• nums.length == n
• 1 <= nums[i] <= 50
• edges.length == n - 1
• edges[i].length == 2
• 0 <= edges[i][0], edges[i][1] <= n - 1
• edges represents a valid tree.

Solutions

Solution 1: Enumeration of Connected Blocks

Assume the number of connected blocks is $k$, then the number of edges to be deleted is $k-1$, and the value of each connected block is $\frac{s}{k}$, where $s$ is the sum of the values of all nodes in $nums$.

We enumerate $k$ from large to small. If there exists a $k$ such that $\frac{s}{k}$ is an integer, and the value of each connected block obtained is equal, then directly return $k-1$. The initial value of $k$ is $\min(n, \frac{s}{mx})$, where $mx$ is the maximum value in $nums$.

The key point is to judge whether for a given $\frac{s}{k}$, it is possible to divide several subtrees such that the value of each subtree is $\frac{s}{k}$.

Here we use the dfs function to judge. We recursively traverse from top to bottom to calculate the value of each subtree. If the sum of the subtree values is exactly $\frac{s}{k}$, it means that the division is successful at this time. We set the value to $0$ and return it to the upper level, indicating that this subtree can be disconnected from the parent node. If the sum of the subtree values is greater than $\frac{s}{k}$, it means that the division fails at this time. We return $-1$, indicating that it cannot be divided.

The time complexity is $O(n \times \sqrt{s})$, where $n$ and $s$ are the length of $nums$ and the sum of the values of all nodes in $nums$, respectively.

Python3JavaC++Go

class Solution:
    def componentValue(self, nums: List[int], edges: List[List[int]]) -> int:
        def dfs(i, fa):
            x = nums[i]
            for j in g[i]:
                if j != fa:
                    y = dfs(j, i)
                    if y == -1:
                        return -1
                    x += y
            if x > t:
                return -1
            return x if x < t else 0

        n = len(nums)
        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        s = sum(nums)
        mx = max(nums)
        for k in range(min(n, s // mx), 1, -1):
            if s % k == 0:
                t = s // k
                if dfs(0, -1) == 0:
                    return k - 1
        return 0

class Solution {
    private List<Integer>[] g;
    private int[] nums;
    private int t;

    public int componentValue(int[] nums, int[][] edges) {
        int n = nums.length;
        g = new List[n];
        this.nums = nums;
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        int s = sum(nums), mx = max(nums);
        for (int k = Math.min(n, s / mx); k > 1; --k) {
            if (s % k == 0) {
                t = s / k;
                if (dfs(0, -1) == 0) {
                    return k - 1;
                }
            }
        }
        return 0;
    }

    private int dfs(int i, int fa) {
        int x = nums[i];
        for (int j : g[i]) {
            if (j != fa) {
                int y = dfs(j, i);
                if (y == -1) {
                    return -1;
                }
                x += y;
            }
        }
        if (x > t) {
            return -1;
        }
        return x < t ? x : 0;
    }

    private int sum(int[] arr) {
        int x = 0;
        for (int v : arr) {
            x += v;
        }
        return x;
    }

    private int max(int[] arr) {
        int x = arr[0];
        for (int v : arr) {
            x = Math.max(x, v);
        }
        return x;
    }
}

class Solution {
public:
    int componentValue(vector<int>& nums, vector<vector<int>>& edges) {
        int n = nums.size();
        int s = accumulate(nums.begin(), nums.end(), 0);
        int mx = *max_element(nums.begin(), nums.end());
        int t = 0;
        unordered_map<int, vector<int>> g;
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        function<int(int, int)> dfs = [&](int i, int fa) -> int {
            int x = nums[i];
            for (int j : g[i]) {
                if (j != fa) {
                    int y = dfs(j, i);
                    if (y == -1) return -1;
                    x += y;
                }
            }
            if (x > t) return -1;
            return x < t ? x : 0;
        };
        for (int k = min(n, s / mx); k > 1; --k) {
            if (s % k == 0) {
                t = s / k;
                if (dfs(0, -1) == 0) {
                    return k - 1;
                }
            }
        }
        return 0;
    }
};

func componentValue(nums []int, edges [][]int) int {
    s, mx := 0, slices.Max(nums)
    for _, x := range nums {
        s += x
    }
    n := len(nums)
    g := make([][]int, n)
    for _, e := range edges {
        a, b := e[0], e[1]
        g[a] = append(g[a], b)
        g[b] = append(g[b], a)
    }
    t := 0
    var dfs func(int, int) int
    dfs = func(i, fa int) int {
        x := nums[i]
        for _, j := range g[i] {
            if j != fa {
                y := dfs(j, i)
                if y == -1 {
                    return -1
                }
                x += y
            }
        }
        if x > t {
            return -1
        }
        if x < t {
            return x
        }
        return 0
    }
    for k := min(n, s/mx); k > 1; k-- {
        if s%k == 0 {
            t = s / k
            if dfs(0, -1) == 0 {
                return k - 1
            }
        }
    }
    return 0
}

Comments