2684. Maximum Number of Moves in a Grid

Description

You are given a 0-indexed m x n matrix grid consisting of positive integers.

You can start at any cell in the first column of the matrix, and traverse the grid in the following way:

• From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.

Return the maximum number of moves that you can perform.

 

Example 1:

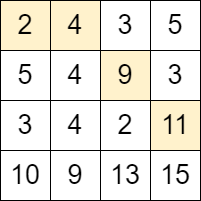
Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
Output: 3
Explanation: We can start at the cell (0, 0) and make the following moves:
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
It can be shown that it is the maximum number of moves that can be made.

Example 2:

Input: grid = [[3,2,4],[2,1,9],[1,1,7]]
Output: 0
Explanation: Starting from any cell in the first column we cannot perform any moves.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 106

Solutions

Solution 1: BFS

We define a queue $q$, and initially add all the row coordinates of the first column to the queue.

Next, we start from the first column and traverse column by column. For each column, we take out all the row coordinates in the queue one by one. For each row coordinate $i$, we get all possible row coordinates $k$ of the next column, and satisfy $grid[i][j] < grid[k][j + 1]$, and add these row coordinates to a new set $t$. If $t$ is empty, it means that we cannot continue to move, so we return the current column number. Otherwise, we assign $t$ to $q$ and continue to traverse the next column.

Finally, if we have traversed all the columns, it means that we can move to the last column, so we return $n - 1$.

The time complexity is $O(m \times n)$, and the space complexity is $O(m)$. Where $m$ and $n$ are the number of rows and columns in the matrix, respectively.

Python3JavaC++GoTypeScript

class Solution:
    def maxMoves(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        q = set(range(m))
        for j in range(n - 1):
            t = set()
            for i in q:
                for k in range(i - 1, i + 2):
                    if 0 <= k < m and grid[i][j] < grid[k][j + 1]:
                        t.add(k)
            if not t:
                return j
            q = t
        return n - 1

class Solution {
    public int maxMoves(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        Set<Integer> q = IntStream.range(0, m).boxed().collect(Collectors.toSet());
        for (int j = 0; j < n - 1; ++j) {
            Set<Integer> t = new HashSet<>();
            for (int i : q) {
                for (int k = i - 1; k <= i + 1; ++k) {
                    if (k >= 0 && k < m && grid[i][j] < grid[k][j + 1]) {
                        t.add(k);
                    }
                }
            }
            if (t.isEmpty()) {
                return j;
            }
            q = t;
        }
        return n - 1;
    }
}

class Solution {
public:
    int maxMoves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        unordered_set<int> q, t;
        for (int i = 0; i < m; ++i) {
            q.insert(i);
        }
        for (int j = 0; j < n - 1; ++j) {
            t.clear();
            for (int i : q) {
                for (int k = i - 1; k <= i + 1; ++k) {
                    if (k >= 0 && k < m && grid[i][j] < grid[k][j + 1]) {
                        t.insert(k);
                    }
                }
            }
            if (t.empty()) {
                return j;
            }
            q.swap(t);
        }
        return n - 1;
    }
};

func maxMoves(grid [][]int) (ans int) {
    m, n := len(grid), len(grid[0])
    q := map[int]bool{}
    for i := range grid {
        q[i] = true
    }
    for j := 0; j < n-1; j++ {
        t := map[int]bool{}
        for i := range q {
            for k := i - 1; k <= i+1; k++ {
                if k >= 0 && k < m && grid[i][j] < grid[k][j+1] {
                    t[k] = true
                }
            }
        }
        if len(t) == 0 {
            return j
        }
        q = t
    }
    return n - 1
}

function maxMoves(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    let q = new Set<number>(Array.from({ length: m }, (_, i) => i));
    for (let j = 0; j < n - 1; ++j) {
        const t = new Set<number>();
        for (const i of q) {
            for (let k = i - 1; k <= i + 1; ++k) {
                if (k >= 0 && k < m && grid[i][j] < grid[k][j + 1]) {
                    t.add(k);
                }
            }
        }
        if (t.size === 0) {
            return j;
        }
        q = t;
    }
    return n - 1;
}

Comments