407. Trapping Rain Water II

Description

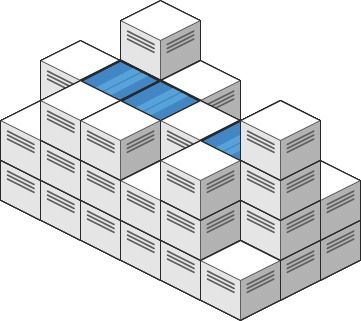
Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

 

Example 1:

Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

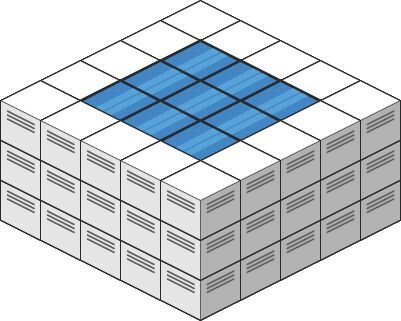
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

 

Constraints:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 104

Solutions

Solution 1

Python3JavaC++Go

class Solution:
    def trapRainWater(self, heightMap: List[List[int]]) -> int:
        m, n = len(heightMap), len(heightMap[0])
        vis = [[False] * n for _ in range(m)]
        pq = []
        for i in range(m):
            for j in range(n):
                if i == 0 or i == m - 1 or j == 0 or j == n - 1:
                    heappush(pq, (heightMap[i][j], i, j))
                    vis[i][j] = True
        ans = 0
        dirs = (-1, 0, 1, 0, -1)
        while pq:
            h, i, j = heappop(pq)
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if x >= 0 and x < m and y >= 0 and y < n and not vis[x][y]:
                    ans += max(0, h - heightMap[x][y])
                    vis[x][y] = True
                    heappush(pq, (max(h, heightMap[x][y]), x, y))
        return ans

class Solution {
    public int trapRainWater(int[][] heightMap) {
        int m = heightMap.length, n = heightMap[0].length;
        boolean[][] vis = new boolean[m][n];
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    pq.offer(new int[] {heightMap[i][j], i, j});
                    vis[i][j] = true;
                }
            }
        }
        int ans = 0;
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!pq.isEmpty()) {
            var p = pq.poll();
            for (int k = 0; k < 4; ++k) {
                int x = p[1] + dirs[k], y = p[2] + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]) {
                    ans += Math.max(0, p[0] - heightMap[x][y]);
                    vis[x][y] = true;
                    pq.offer(new int[] {Math.max(p[0], heightMap[x][y]), x, y});
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        using tii = tuple<int, int, int>;
        priority_queue<tii, vector<tii>, greater<tii>> pq;
        int m = heightMap.size(), n = heightMap[0].size();
        bool vis[m][n];
        memset(vis, 0, sizeof vis);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    pq.emplace(heightMap[i][j], i, j);
                    vis[i][j] = true;
                }
            }
        }
        int ans = 0;
        int dirs[5] = {-1, 0, 1, 0, -1};
        while (!pq.empty()) {
            auto [h, i, j] = pq.top();
            pq.pop();
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]) {
                    ans += max(0, h - heightMap[x][y]);
                    vis[x][y] = true;
                    pq.emplace(max(heightMap[x][y], h), x, y);
                }
            }
        }
        return ans;
    }
};

func trapRainWater(heightMap [][]int) (ans int) {
    m, n := len(heightMap), len(heightMap[0])
    pq := hp{}
    vis := make([][]bool, m)
    for i, row := range heightMap {
        vis[i] = make([]bool, n)
        for j, v := range row {
            if i == 0 || i == m-1 || j == 0 || j == n-1 {
                heap.Push(&pq, tuple{v, i, j})
                vis[i][j] = true
            }
        }
    }
    dirs := []int{-1, 0, 1, 0, -1}
    for len(pq) > 0 {
        p := heap.Pop(&pq).(tuple)
        for k := 0; k < 4; k++ {
            x, y := p.i+dirs[k], p.j+dirs[k+1]
            if x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] {
                ans += max(0, p.v-heightMap[x][y])
                vis[x][y] = true
                heap.Push(&pq, tuple{max(p.v, heightMap[x][y]), x, y})
            }
        }
    }
    return
}

type tuple struct{ v, i, j int }
type hp []tuple

func (h hp) Len() int           { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].v < h[j].v }
func (h hp) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any)        { *h = append(*h, v.(tuple)) }
func (h *hp) Pop() any          { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }

Comments