2673. Make Costs of Paths Equal in a Binary Tree

Description

You are given an integer n representing the number of nodes in a perfect binary tree consisting of nodes numbered from 1 to n. The root of the tree is node 1 and each node i in the tree has two children where the left child is the node 2 * i and the right child is 2 * i + 1.

Each node in the tree also has a cost represented by a given 0-indexed integer array cost of size n where cost[i] is the cost of node i + 1. You are allowed to increment the cost of any node by 1 any number of times.

Return the minimum number of increments you need to make the cost of paths from the root to each leaf node equal.

Note:

A perfect binary tree is a tree where each node, except the leaf nodes, has exactly 2 children.
The cost of a path is the sum of costs of nodes in the path.

Example 1:

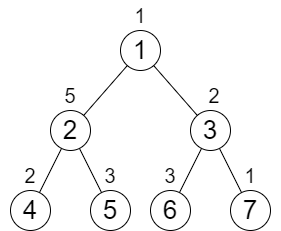
Input: n = 7, cost = [1,5,2,2,3,3,1]
Output: 6
Explanation: We can do the following increments:
- Increase the cost of node 4 one time.
- Increase the cost of node 3 three times.
- Increase the cost of node 7 two times.
Each path from the root to a leaf will have a total cost of 9.
The total increments we did is 1 + 3 + 2 = 6.
It can be shown that this is the minimum answer we can achieve.

Example 2:

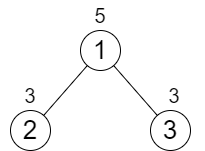
Input: n = 3, cost = [5,3,3]
Output: 0
Explanation: The two paths already have equal total costs, so no increments are needed.

Constraints:

3 <= n <= 10⁵
n + 1 is a power of 2
cost.length == n
1 <= cost[i] <= 10⁴

Solutions

Solution 1: Greedy Algorithm

According to the problem description, we need to calculate the minimum number of increments to make the path values from the root node to each leaf node equal.

The path values from the root node to each leaf node being equal is actually equivalent to the path values from any node as the root of a subtree to each leaf node of that subtree being equal.

Why is that? We can prove it by contradiction. Suppose there is a node $x$, and the path values from it as the root of a subtree to some leaf nodes are not equal. Then there exists a situation where the path values from the root node to the leaf nodes are not equal, which contradicts the condition "the path values from the root node to each leaf node are equal". Therefore, the assumption is not valid, and the path values from any node as the root of a subtree to each leaf node of that subtree are equal.

We can start from the bottom of the tree and calculate the number of increments layer by layer. For each non-leaf node, we can calculate the path values of its left and right child nodes. The number of increments is the difference between the two path values, and then update the path values of the left and right child nodes to the larger one of the two.

Finally, return the total number of increments.

The time complexity is $O(n)$, where $n$ is the number of nodes. The space complexity is $O(1)$.

Python3JavaC++GoTypeScript

class Solution:
    def minIncrements(self, n: int, cost: List[int]) -> int:
        ans = 0
        for i in range(n >> 1, 0, -1):
            l, r = i << 1, i << 1 | 1
            ans += abs(cost[l - 1] - cost[r - 1])
            cost[i - 1] += max(cost[l - 1], cost[r - 1])
        return ans

class Solution {
    public int minIncrements(int n, int[] cost) {
        int ans = 0;
        for (int i = n >> 1; i > 0; --i) {
            int l = i << 1, r = i << 1 | 1;
            ans += Math.abs(cost[l - 1] - cost[r - 1]);
            cost[i - 1] += Math.max(cost[l - 1], cost[r - 1]);
        }
        return ans;
    }
}

class Solution {
public:
    int minIncrements(int n, vector<int>& cost) {
        int ans = 0;
        for (int i = n >> 1; i > 0; --i) {
            int l = i << 1, r = i << 1 | 1;
            ans += abs(cost[l - 1] - cost[r - 1]);
            cost[i - 1] += max(cost[l - 1], cost[r - 1]);
        }
        return ans;
    }
};

func minIncrements(n int, cost []int) (ans int) {
    for i := n >> 1; i > 0; i-- {
        l, r := i<<1, i<<1|1
        ans += abs(cost[l-1] - cost[r-1])
        cost[i-1] += max(cost[l-1], cost[r-1])
    }
    return
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

function minIncrements(n: number, cost: number[]): number {
    let ans = 0;
    for (let i = n >> 1; i; --i) {
        const [l, r] = [i << 1, (i << 1) | 1];
        ans += Math.abs(cost[l - 1] - cost[r - 1]);
        cost[i - 1] += Math.max(cost[l - 1], cost[r - 1]);
    }
    return ans;
}

2673. Make Costs of Paths Equal in a Binary Tree

Description

Solutions

Solution 1: Greedy Algorithm

Comments