431. Encode N-ary Tree to Binary Tree 🔒

Description

Design an algorithm to encode an N-ary tree into a binary tree and decode the binary tree to get the original N-ary tree. An N-ary tree is a rooted tree in which each node has no more than N children. Similarly, a binary tree is a rooted tree in which each node has no more than 2 children. There is no restriction on how your encode/decode algorithm should work. You just need to ensure that an N-ary tree can be encoded to a binary tree and this binary tree can be decoded to the original N-nary tree structure.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See following example).

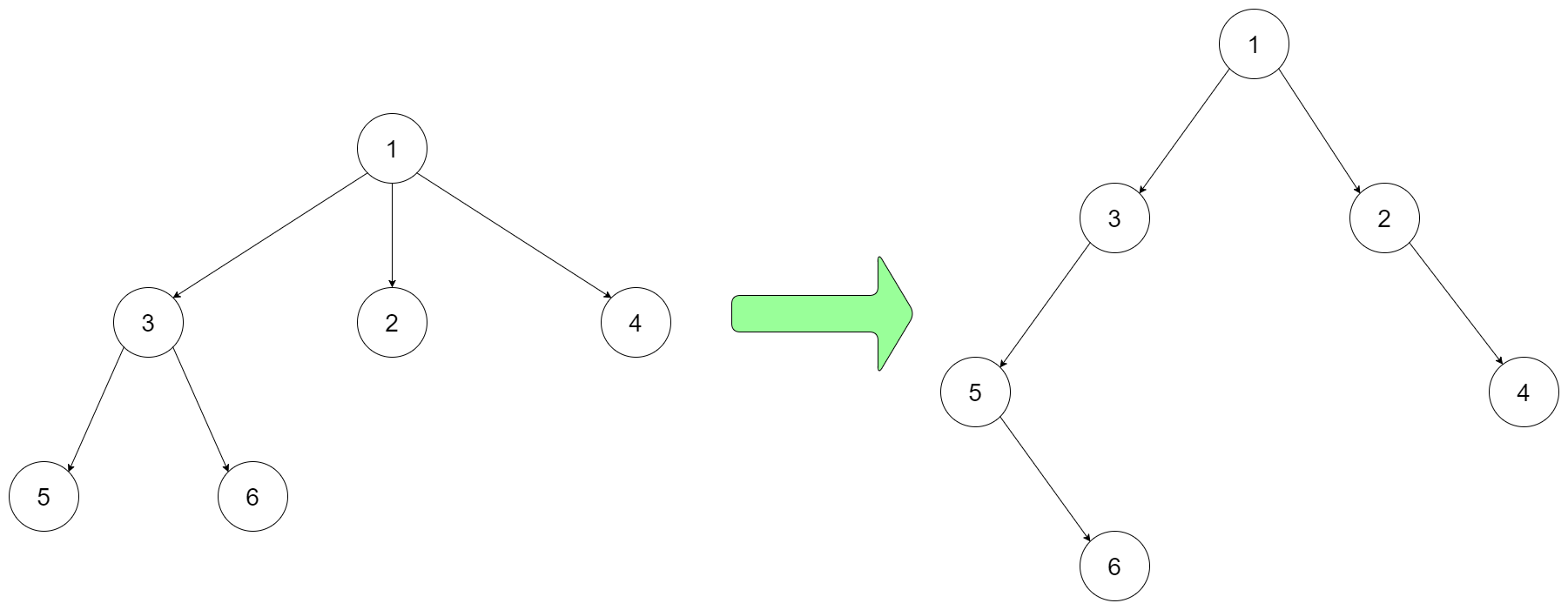
For example, you may encode the following 3-ary tree to a binary tree in this way:

Input: root = [1,null,3,2,4,null,5,6]

Note that the above is just an example which might or might not work. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: [1,null,3,2,4,null,5,6]

Example 2:

Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]

Example 3:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 10⁴].
0 <= Node.val <= 10⁴
The height of the n-ary tree is less than or equal to 1000
Do not use class member/global/static variables to store states. Your encode and decode algorithms should be stateless.

Solutions

Solution 1: Recursion

We can point the left pointer of the binary tree to the first child of the N-ary tree and the right pointer of the binary tree to the next sibling node of the N-ary tree.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the N-ary tree.

Python3JavaC++GoTypeScript

"""
# Definition for a Node.
class Node:
    def __init__(self, val: Optional[int] = None, children: Optional[List['Node']] = None):
        self.val = val
        self.children = children
"""

"""
# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
"""


class Codec:
    # Encodes an n-ary tree to a binary tree.
    def encode(self, root: "Optional[Node]") -> Optional[TreeNode]:
        if root is None:
            return None
        node = TreeNode(root.val)
        if not root.children:
            return node
        left = self.encode(root.children[0])
        node.left = left
        for child in root.children[1:]:
            left.right = self.encode(child)
            left = left.right
        return node

    # Decodes your binary tree to an n-ary tree.
    def decode(self, data: Optional[TreeNode]) -> "Optional[Node]":
        if data is None:
            return None
        node = Node(data.val, [])
        if data.left is None:
            return node
        left = data.left
        while left:
            node.children.append(self.decode(left))
            left = left.right
        return node


# Your Codec object will be instantiated and called as such:
# codec = Codec()
# codec.decode(codec.encode(root))

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

class Codec {
    // Encodes an n-ary tree to a binary tree.
    public TreeNode encode(Node root) {
        if (root == null) {
            return null;
        }
        TreeNode node = new TreeNode(root.val);
        if (root.children == null || root.children.isEmpty()) {
            return node;
        }
        TreeNode left = encode(root.children.get(0));
        node.left = left;
        for (int i = 1; i < root.children.size(); i++) {
            left.right = encode(root.children.get(i));
            left = left.right;
        }
        return node;
    }

    // Decodes your binary tree to an n-ary tree.
    public Node decode(TreeNode data) {
        if (data == null) {
            return null;
        }
        Node node = new Node(data.val, new ArrayList<>());
        if (data.left == null) {
            return node;
        }
        TreeNode left = data.left;
        while (left != null) {
            node.children.add(decode(left));
            left = left.right;
        }
        return node;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.decode(codec.encode(root));