Skip to content

2123. Minimum Operations to Remove Adjacent Ones in Matrix πŸ”’

Description

You are given a 0-indexed binary matrix grid. In one operation, you can flip any 1 in grid to be 0.

A binary matrix is well-isolated if there is no 1 in the matrix that is 4-directionally connected (i.e., horizontal and vertical) to another 1.

Return the minimum number of operations to make grid well-isolated.

 

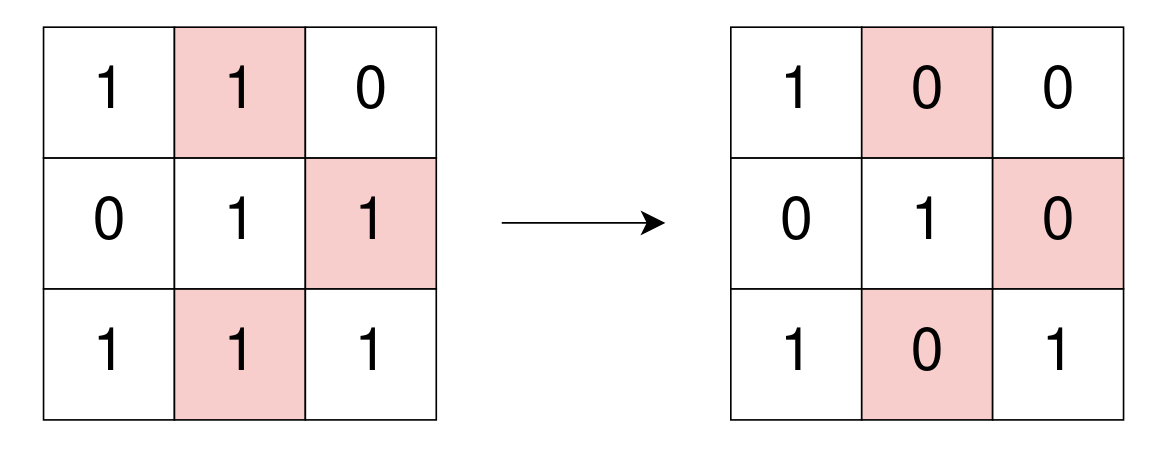
Example 1:

Input: grid = [[1,1,0],[0,1,1],[1,1,1]]
Output: 3
Explanation: Use 3 operations to change grid[0][1], grid[1][2], and grid[2][1] to 0.
After, no more 1's are 4-directionally connected and grid is well-isolated.

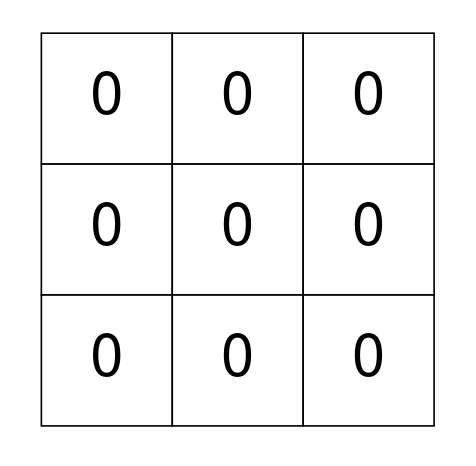
Example 2:

Input: grid = [[0,0,0],[0,0,0],[0,0,0]]
Output: 0
Explanation: There are no 1's in grid and it is well-isolated.
No operations were done so return 0.

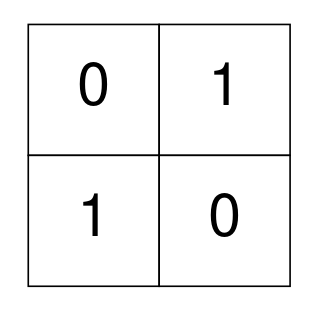
Example 3:

Input: grid = [[0,1],[1,0]]
Output: 0
Explanation: None of the 1's are 4-directionally connected and grid is well-isolated.
No operations were done so return 0.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 300
  • grid[i][j] is either 0 or 1.

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
    def minimumOperations(self, grid: List[List[int]]) -> int:
        def find(i: int) -> int:
            for j in g[i]:
                if j not in vis:
                    vis.add(j)
                    if match[j] == -1 or find(match[j]):
                        match[j] = i
                        return 1
            return 0

        g = defaultdict(list)
        m, n = len(grid), len(grid[0])
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                if (i + j) % 2 and v:
                    x = i * n + j
                    if i < m - 1 and grid[i + 1][j]:
                        g[x].append(x + n)
                    if i and grid[i - 1][j]:
                        g[x].append(x - n)
                    if j < n - 1 and grid[i][j + 1]:
                        g[x].append(x + 1)
                    if j and grid[i][j - 1]:
                        g[x].append(x - 1)

        match = [-1] * (m * n)
        ans = 0
        for i in g.keys():
            vis = set()
            ans += find(i)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    private Map<Integer, List<Integer>> g = new HashMap<>();
    private Set<Integer> vis = new HashSet<>();
    private int[] match;

    public int minimumOperations(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if ((i + j) % 2 == 1 && grid[i][j] == 1) {
                    int x = i * n + j;
                    if (i < m - 1 && grid[i + 1][j] == 1) {
                        g.computeIfAbsent(x, z -> new ArrayList<>()).add(x + n);
                    }
                    if (i > 0 && grid[i - 1][j] == 1) {
                        g.computeIfAbsent(x, z -> new ArrayList<>()).add(x - n);
                    }
                    if (j < n - 1 && grid[i][j + 1] == 1) {
                        g.computeIfAbsent(x, z -> new ArrayList<>()).add(x + 1);
                    }
                    if (j > 0 && grid[i][j - 1] == 1) {
                        g.computeIfAbsent(x, z -> new ArrayList<>()).add(x - 1);
                    }
                }
            }
        }
        match = new int[m * n];
        Arrays.fill(match, -1);
        int ans = 0;
        for (int i : g.keySet()) {
            ans += find(i);
            vis.clear();
        }
        return ans;
    }

    private int find(int i) {
        for (int j : g.get(i)) {
            if (vis.add(j)) {
                if (match[j] == -1 || find(match[j]) == 1) {
                    match[j] = i;
                    return 1;
                }
            }
        }
        return 0;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
public:
    int minimumOperations(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<int> match(m * n, -1);
        unordered_set<int> vis;
        unordered_map<int, vector<int>> g;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if ((i + j) % 2 && grid[i][j]) {
                    int x = i * n + j;
                    if (i < m - 1 && grid[i + 1][j]) {
                        g[x].push_back(x + n);
                    }
                    if (i && grid[i - 1][j]) {
                        g[x].push_back(x - n);
                    }
                    if (j < n - 1 && grid[i][j + 1]) {
                        g[x].push_back(x + 1);
                    }
                    if (j && grid[i][j - 1]) {
                        g[x].push_back(x - 1);
                    }
                }
            }
        }
        int ans = 0;
        function<int(int)> find = [&](int i) -> int {
            for (int& j : g[i]) {
                if (!vis.count(j)) {
                    vis.insert(j);
                    if (match[j] == -1 || find(match[j])) {
                        match[j] = i;
                        return 1;
                    }
                }
            }
            return 0;
        };
        for (auto& [i, _] : g) {
            ans += find(i);
            vis.clear();
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
func minimumOperations(grid [][]int) (ans int) {
    m, n := len(grid), len(grid[0])
    vis := map[int]bool{}
    match := make([]int, m*n)
    for i := range match {
        match[i] = -1
    }
    g := map[int][]int{}
    for i, row := range grid {
        for j, v := range row {
            if (i+j)&1 == 1 && v == 1 {
                x := i*n + j
                if i < m-1 && grid[i+1][j] == 1 {
                    g[x] = append(g[x], x+n)
                }
                if i > 0 && grid[i-1][j] == 1 {
                    g[x] = append(g[x], x-n)
                }
                if j < n-1 && grid[i][j+1] == 1 {
                    g[x] = append(g[x], x+1)
                }
                if j > 0 && grid[i][j-1] == 1 {
                    g[x] = append(g[x], x-1)
                }
            }
        }
    }
    var find func(int) int
    find = func(i int) int {
        for _, j := range g[i] {
            if !vis[j] {
                vis[j] = true
                if match[j] == -1 || find(match[j]) == 1 {
                    match[j] = i
                    return 1
                }
            }
        }
        return 0
    }
    for i := range g {
        ans += find(i)
        vis = map[int]bool{}
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
function minimumOperations(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const match: number[] = Array(m * n).fill(-1);
    const vis: Set<number> = new Set();
    const g: Map<number, number[]> = new Map();
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if ((i + j) % 2 && grid[i][j]) {
                const x = i * n + j;
                g.set(x, []);
                if (i < m - 1 && grid[i + 1][j]) {
                    g.get(x)!.push(x + n);
                }
                if (i && grid[i - 1][j]) {
                    g.get(x)!.push(x - n);
                }
                if (j < n - 1 && grid[i][j + 1]) {
                    g.get(x)!.push(x + 1);
                }
                if (j && grid[i][j - 1]) {
                    g.get(x)!.push(x - 1);
                }
            }
        }
    }
    const find = (i: number): number => {
        for (const j of g.get(i)!) {
            if (!vis.has(j)) {
                vis.add(j);
                if (match[j] === -1 || find(match[j])) {
                    match[j] = i;
                    return 1;
                }
            }
        }
        return 0;
    };
    let ans = 0;
    for (const i of g.keys()) {
        ans += find(i);
        vis.clear();
    }
    return ans;
}

Comments