590. N-ary Tree Postorder Traversal

Description

Given the root of an n-ary tree, return the postorder traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)

 

Example 1:

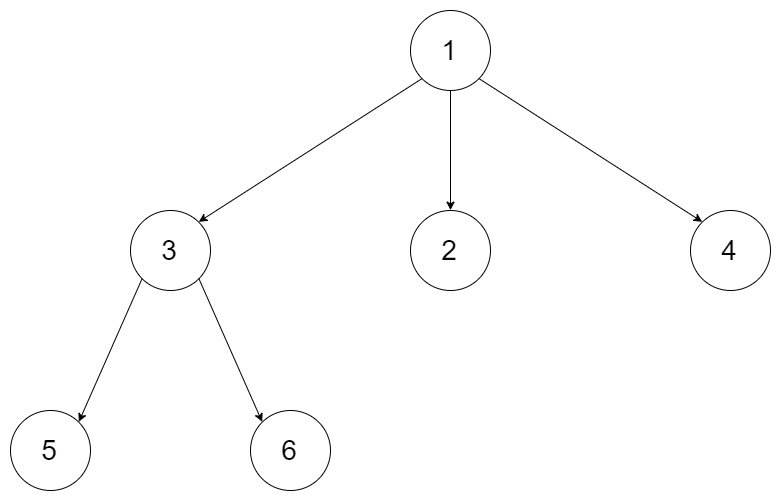
Input: root = [1,null,3,2,4,null,5,6]
Output: [5,6,3,2,4,1]

Example 2:

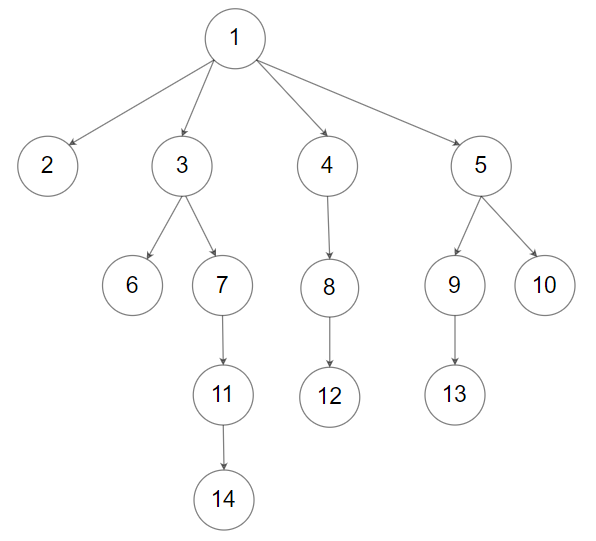
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [2,6,14,11,7,3,12,8,4,13,9,10,5,1]

 

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• 0 <= Node.val <= 104
• The height of the n-ary tree is less than or equal to 1000.

 

Follow up: Recursive solution is trivial, could you do it iteratively?

Solutions

Solution 1: Recursion

We can recursively traverse the entire tree. For each node, we first recursively call the function for each of the node's children, then add the node's value to the answer.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.

Python3JavaC++GoTypeScript

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""


class Solution:
    def postorder(self, root: 'Node') -> List[int]:
        def dfs(root):
            if root is None:
                return
            for child in root.children:
                dfs(child)
            ans.append(root.val)

        ans = []
        dfs(root)
        return ans

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    private List<Integer> ans = new ArrayList<>();

    public List<Integer> postorder(Node root) {
        dfs(root);
        return ans;
    }

    private void dfs(Node root) {
        if (root == null) {
            return;
        }
        for (Node child : root.children) {
            dfs(child);
        }
        ans.add(root.val);
    }
}

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    vector<int> postorder(Node* root) {
        vector<int> ans;
        function<void(Node*)> dfs = [&](Node* root) {
            if (!root) {
                return;
            }
            for (auto& child : root->children) {
                dfs(child);
            }
            ans.push_back(root->val);
        };
        dfs(root);
        return ans;
    }
};

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Children []*Node
 * }
 */

func postorder(root *Node) (ans []int) {
    var dfs func(*Node)
    dfs = func(root *Node) {
        if root == nil {
            return
        }
        for _, child := range root.Children {
            dfs(child)
        }
        ans = append(ans, root.Val)
    }
    dfs(root)
    return
}

/**
 * Definition for node.
 * class Node {
 *     val: number
 *     children: Node[]
 *     constructor(val?: number) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.children = []
 *     }
 * }
 */

function postorder(root: Node | null): number[] {
    const ans: number[] = [];
    const dfs = (root: Node | null) => {
        if (!root) {
            return;
        }
        for (const child of root.children) {
            dfs(child);
        }
        ans.push(root.val);
    };
    dfs(root);
    return ans;
}

Solution 2: Iteration (Stack Implementation)

We can also solve this problem iteratively.

We use a stack to help us get the post-order traversal. We first push the root node into the stack. Since the post-order traversal is left subtree, right subtree, root, and the characteristic of the stack is first in last out, we first add the node's value to the answer, then push each of the node's children into the stack in the order from left to right. This way, we can get the traversal result of root, right subtree, left subtree. Finally, we reverse the answer to get the post-order traversal result.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.

Python3JavaC++GoTypeScript

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""


class Solution:
    def postorder(self, root: 'Node') -> List[int]:
        ans = []
        if root is None:
            return ans
        stk = [root]
        while stk:
            node = stk.pop()
            ans.append(node.val)
            for child in node.children:
                stk.append(child)
        return ans[::-1]

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List<Integer> postorder(Node root) {
        LinkedList<Integer> ans = new LinkedList<>();
        if (root == null) {
            return ans;
        }
        Deque<Node> stk = new ArrayDeque<>();
        stk.offer(root);
        while (!stk.isEmpty()) {
            root = stk.pollLast();
            ans.addFirst(root.val);
            for (Node child : root.children) {
                stk.offer(child);
            }
        }
        return ans;
    }
}

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    vector<int> postorder(Node* root) {
        vector<int> ans;
        if (!root) {
            return ans;
        }
        stack<Node*> stk{{root}};
        while (!stk.empty()) {
            root = stk.top();
            ans.push_back(root->val);
            stk.pop();
            for (Node* child : root->children) {
                stk.push(child);
            }
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Children []*Node
 * }
 */

func postorder(root *Node) []int {
    var ans []int
    if root == nil {
        return ans
    }
    stk := []*Node{root}
    for len(stk) > 0 {
        root = stk[len(stk)-1]
        stk = stk[:len(stk)-1]
        ans = append([]int{root.Val}, ans...)
        for _, child := range root.Children {
            stk = append(stk, child)
        }
    }
    return ans
}

/**
 * Definition for node.
 * class Node {
 *     val: number
 *     children: Node[]
 *     constructor(val?: number) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.children = []
 *     }
 * }
 */

function postorder(root: Node | null): number[] {
    const ans: number[] = [];
    if (!root) {
        return ans;
    }
    const stk: Node[] = [root];
    while (stk.length) {
        const { val, children } = stk.pop()!;
        ans.push(val);
        stk.push(...children);
    }
    return ans.reverse();
}

Comments