Skip to content

1582. Special Positions in a Binary Matrix

Description

Given an m x n binary matrix mat, return the number of special positions in mat.

A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).

 

Example 1:

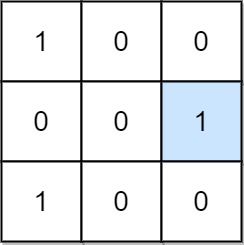
Input: mat = [[1,0,0],[0,0,1],[1,0,0]]
Output: 1
Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.

Example 2:

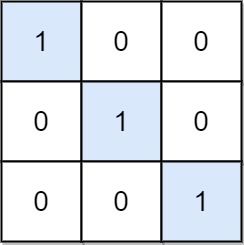
Input: mat = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3
Explanation: (0, 0), (1, 1) and (2, 2) are special positions.

 

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 100
  • mat[i][j] is either 0 or 1.

Solutions

Solution 1: Counting

We can use two arrays, $\textit{rows}$ and $\textit{cols}$, to record the number of $1$s in each row and each column, respectively.

Then, we traverse the matrix. For each $1$, we check whether there is only one $1$ in its row and column. If so, we increment the answer by one.

After the traversal, we return the answer.

The time complexity is $O(m \times n)$, and the space complexity is $O(m + n)$. Here, $m$ and $n$ are the number of rows and columns of the matrix $\textit{mat}$, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
    def numSpecial(self, mat: List[List[int]]) -> int:
        rows = [0] * len(mat)
        cols = [0] * len(mat[0])
        for i, row in enumerate(mat):
            for j, x in enumerate(row):
                rows[i] += x
                cols[j] += x
        ans = 0
        for i, row in enumerate(mat):
            for j, x in enumerate(row):
                ans += x == 1 and rows[i] == 1 and cols[j] == 1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int numSpecial(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[] rows = new int[m];
        int[] cols = new int[n];

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                rows[i] += mat[i][j];
                cols[j] += mat[i][j];
            }
        }

        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1) {
                    ans++;
                }
            }
        }

        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int numSpecial(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<int> rows(m);
        vector<int> cols(n);

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                rows[i] += mat[i][j];
                cols[j] += mat[i][j];
            }
        }

        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1) {
                    ans++;
                }
            }
        }

        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
func numSpecial(mat [][]int) (ans int) {
    rows := make([]int, len(mat))
    cols := make([]int, len(mat[0]))
    for i, row := range mat {
        for j, x := range row {
            rows[i] += x
            cols[j] += x
        }
    }
    for i, row := range mat {
        for j, x := range row {
            if x == 1 && rows[i] == 1 && cols[j] == 1 {
                ans++
            }
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
function numSpecial(mat: number[][]): number {
    const m = mat.length;
    const n = mat[0].length;
    const rows: number[] = Array(m).fill(0);
    const cols: number[] = Array(n).fill(0);
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            rows[i] += mat[i][j];
            cols[j] += mat[i][j];
        }
    }
    let ans = 0;
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (mat[i][j] === 1 && rows[i] === 1 && cols[j] === 1) {
                ++ans;
            }
        }
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
impl Solution {
    pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {
        let m = mat.len();
        let n = mat[0].len();
        let mut rows = vec![0; m];
        let mut cols = vec![0; n];
        for i in 0..m {
            for j in 0..n {
                rows[i] += mat[i][j];
                cols[j] += mat[i][j];
            }
        }

        let mut ans = 0;
        for i in 0..m {
            for j in 0..n {
                if mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1 {
                    ans += 1;
                }
            }
        }
        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int numSpecial(int** mat, int matSize, int* matColSize) {
    int m = matSize, n = matColSize[0];
    int rows[m];
    int cols[n];
    memset(rows, 0, sizeof(rows));
    memset(cols, 0, sizeof(cols));

    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            rows[i] += mat[i][j];
            cols[j] += mat[i][j];
        }
    }

    int ans = 0;
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            if (mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1) {
                ans++;
            }
        }
    }

    return ans;

Comments