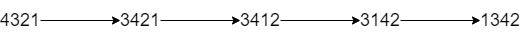1505. Minimum Possible Integer After at Most K Adjacent Swaps On Digits

Description

You are given a string num representing the digits of a very large integer and an integer k. You are allowed to swap any two adjacent digits of the integer at most k times.

Return the minimum integer you can obtain also as a string.

 

Example 1:

Input: num = "4321", k = 4
Output: "1342"
Explanation: The steps to obtain the minimum integer from 4321 with 4 adjacent swaps are shown.

Example 2:

Input: num = "100", k = 1
Output: "010"
Explanation: It's ok for the output to have leading zeros, but the input is guaranteed not to have any leading zeros.

Example 3:

Input: num = "36789", k = 1000
Output: "36789"
Explanation: We can keep the number without any swaps.

 

Constraints:

• 1 <= num.length <= 3 * 104
• num consists of only digits and does not contain leading zeros.
• 1 <= k <= 109

Solutions

Solution 1

Python3JavaC++Go

class BinaryIndexedTree:
    def __init__(self, n):
        self.n = n
        self.c = [0] * (n + 1)

    @staticmethod
    def lowbit(x):
        return x & -x

    def update(self, x, delta):
        while x <= self.n:
            self.c[x] += delta
            x += BinaryIndexedTree.lowbit(x)

    def query(self, x):
        s = 0
        while x:
            s += self.c[x]
            x -= BinaryIndexedTree.lowbit(x)
        return s


class Solution:
    def minInteger(self, num: str, k: int) -> str:
        pos = defaultdict(deque)
        for i, v in enumerate(num, 1):
            pos[int(v)].append(i)
        ans = []
        n = len(num)
        tree = BinaryIndexedTree(n)
        for i in range(1, n + 1):
            for v in range(10):
                q = pos[v]
                if q:
                    j = q[0]
                    dist = tree.query(n) - tree.query(j) + j - i
                    if dist <= k:
                        k -= dist
                        q.popleft()
                        ans.append(str(v))
                        tree.update(j, 1)
                        break
        return ''.join(ans)

class Solution {
    public String minInteger(String num, int k) {
        Queue<Integer>[] pos = new Queue[10];
        for (int i = 0; i < 10; ++i) {
            pos[i] = new ArrayDeque<>();
        }
        int n = num.length();
        for (int i = 0; i < n; ++i) {
            pos[num.charAt(i) - '0'].offer(i + 1);
        }
        StringBuilder ans = new StringBuilder();
        BinaryIndexedTree tree = new BinaryIndexedTree(n);
        for (int i = 1; i <= n; ++i) {
            for (int v = 0; v < 10; ++v) {
                if (!pos[v].isEmpty()) {
                    Queue<Integer> q = pos[v];
                    int j = q.peek();
                    int dist = tree.query(n) - tree.query(j) + j - i;
                    if (dist <= k) {
                        k -= dist;
                        q.poll();
                        ans.append(v);
                        tree.update(j, 1);
                        break;
                    }
                }
            }
        }
        return ans.toString();
    }
}

class BinaryIndexedTree {
    private int n;
    private int[] c;

    public BinaryIndexedTree(int n) {
        this.n = n;
        c = new int[n + 1];
    }

    public void update(int x, int delta) {
        while (x <= n) {
            c[x] += delta;
            x += lowbit(x);
        }
    }

    public int query(int x) {
        int s = 0;
        while (x > 0) {
            s += c[x];
            x -= lowbit(x);
        }
        return s;
    }

    public static int lowbit(int x) {
        return x & -x;
    }
}

class BinaryIndexedTree {
public:
    int n;
    vector<int> c;

    BinaryIndexedTree(int _n)
        : n(_n)
        , c(_n + 1) {}

    void update(int x, int delta) {
        while (x <= n) {
            c[x] += delta;
            x += lowbit(x);
        }
    }

    int query(int x) {
        int s = 0;
        while (x > 0) {
            s += c[x];
            x -= lowbit(x);
        }
        return s;
    }

    int lowbit(int x) {
        return x & -x;
    }
};

class Solution {
public:
    string minInteger(string num, int k) {
        vector<queue<int>> pos(10);
        int n = num.size();
        for (int i = 0; i < n; ++i) pos[num[i] - '0'].push(i + 1);
        BinaryIndexedTree* tree = new BinaryIndexedTree(n);
        string ans = "";
        for (int i = 1; i <= n; ++i) {
            for (int v = 0; v < 10; ++v) {
                auto& q = pos[v];
                if (!q.empty()) {
                    int j = q.front();
                    int dist = tree->query(n) - tree->query(j) + j - i;
                    if (dist <= k) {
                        k -= dist;
                        q.pop();
                        ans += (v + '0');
                        tree->update(j, 1);
                        break;
                    }
                }
            }
        }
        return ans;
    }
};

type BinaryIndexedTree struct {
    n int
    c []int
}

func newBinaryIndexedTree(n int) *BinaryIndexedTree {
    c := make([]int, n+1)
    return &BinaryIndexedTree{n, c}
}

func (this *BinaryIndexedTree) lowbit(x int) int {
    return x & -x
}

func (this *BinaryIndexedTree) update(x, delta int) {
    for x <= this.n {
        this.c[x] += delta
        x += this.lowbit(x)
    }
}

func (this *BinaryIndexedTree) query(x int) int {
    s := 0
    for x > 0 {
        s += this.c[x]
        x -= this.lowbit(x)
    }
    return s
}

func minInteger(num string, k int) string {
    pos := make([][]int, 10)
    for i, c := range num {
        pos[c-'0'] = append(pos[c-'0'], i+1)
    }
    n := len(num)
    tree := newBinaryIndexedTree(n)
    var ans strings.Builder
    for i := 1; i <= n; i++ {
        for v := 0; v < 10; v++ {
            if len(pos[v]) > 0 {
                j := pos[v][0]
                dist := tree.query(n) - tree.query(j) + j - i
                if dist <= k {
                    k -= dist
                    pos[v] = pos[v][1:]
                    ans.WriteByte(byte(v + '0'))
                    tree.update(j, 1)
                    break
                }
            }
        }
    }
    return ans.String()
}

Comments