508. Most Frequent Subtree Sum

Description

Given the root of a binary tree, return the most frequent subtree sum. If there is a tie, return all the values with the highest frequency in any order.

The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).

 

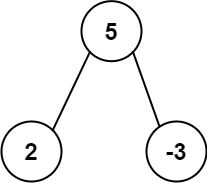
Example 1:

Input: root = [5,2,-3]
Output: [2,-3,4]

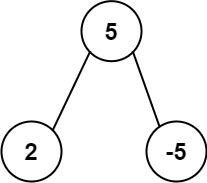
Example 2:

Input: root = [5,2,-5]
Output: [2]

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -105 <= Node.val <= 105

Solutions

Solution 1: Hash Table + DFS

We can use a hash table $\textit{cnt}$ to record the frequency of each subtree sum. Then, we use depth-first search (DFS) to traverse the entire tree, calculate the sum of elements for each subtree, and update $\textit{cnt}$.

Finally, we traverse $\textit{cnt}$ to find all subtree sums that appear most frequently.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.

Python3JavaC++GoTypeScriptRust

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findFrequentTreeSum(self, root: Optional[TreeNode]) -> List[int]:
        def dfs(root: Optional[TreeNode]) -> int:
            if root is None:
                return 0
            l, r = dfs(root.left), dfs(root.right)
            s = l + r + root.val
            cnt[s] += 1
            return s

        cnt = Counter()
        dfs(root)
        mx = max(cnt.values())
        return [k for k, v in cnt.items() if v == mx]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private Map<Integer, Integer> cnt = new HashMap<>();
    private int mx;

    public int[] findFrequentTreeSum(TreeNode root) {
        dfs(root);
        List<Integer> ans = new ArrayList<>();
        for (var e : cnt.entrySet()) {
            if (e.getValue() == mx) {
                ans.add(e.getKey());
            }
        }
        return ans.stream().mapToInt(i -> i).toArray();
    }

    private int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int s = root.val + dfs(root.left) + dfs(root.right);
        mx = Math.max(mx, cnt.merge(s, 1, Integer::sum));
        return s;
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> findFrequentTreeSum(TreeNode* root) {
        unordered_map<int, int> cnt;
        int mx = 0;
        function<int(TreeNode*)> dfs = [&](TreeNode* root) -> int {
            if (!root) {
                return 0;
            }
            int s = root->val + dfs(root->left) + dfs(root->right);
            mx = max(mx, ++cnt[s]);
            return s;
        };
        dfs(root);
        vector<int> ans;
        for (const auto& [k, v] : cnt) {
            if (v == mx) {
                ans.push_back(k);
            }
        }
        return ans;
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func findFrequentTreeSum(root *TreeNode) (ans []int) {
    cnt := map[int]int{}
    var mx int
    var dfs func(*TreeNode) int
    dfs = func(root *TreeNode) int {
        if root == nil {
            return 0
        }
        s := root.Val + dfs(root.Left) + dfs(root.Right)
        cnt[s]++
        mx = max(mx, cnt[s])
        return s
    }
    dfs(root)
    for k, v := range cnt {
        if v == mx {
            ans = append(ans, k)
        }
    }
    return
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function findFrequentTreeSum(root: TreeNode | null): number[] {
    const cnt = new Map<number, number>();
    let mx = 0;
    const dfs = (root: TreeNode | null): number => {
        if (!root) {
            return 0;
        }
        const { val, left, right } = root;
        const s = val + dfs(left) + dfs(right);
        cnt.set(s, (cnt.get(s) ?? 0) + 1);
        mx = Math.max(mx, cnt.get(s)!);
        return s;
    };
    dfs(root);
    return Array.from(cnt.entries())
        .filter(([_, c]) => c === mx)
        .map(([s, _]) => s);
}

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::collections::HashMap;
use std::rc::Rc;

impl Solution {
    pub fn find_frequent_tree_sum(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
        fn dfs(root: Option<Rc<RefCell<TreeNode>>>, cnt: &mut HashMap<i32, i32>) -> i32 {
            if let Some(node) = root {
                let l = dfs(node.borrow().left.clone(), cnt);
                let r = dfs(node.borrow().right.clone(), cnt);
                let s = l + r + node.borrow().val;
                *cnt.entry(s).or_insert(0) += 1;
                s
            } else {
                0
            }
        }

        let mut cnt = HashMap::new();
        dfs(root, &mut cnt);

        let mx = cnt.values().cloned().max().unwrap_or(0);
        cnt.into_iter()
            .filter(|&(_, v)| v == mx)
            .map(|(k, _)| k)
            .collect()
    }
}

Comments