2090. K Radius Subarray Averages

Description

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.

Example 1:

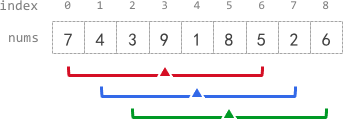
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.

Example 2:

Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input: nums = [8], k = 100000
Output: [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0.

Constraints:

n == nums.length
1 <= n <= 10⁵
0 <= nums[i], k <= 10⁵

Solutions

Solution 1: Sliding Window

The number of elements in a subarray with radius $k$ is $k \times 2 + 1$. Therefore, we can redefine $k$ as $k \times 2 + 1$.

We create an answer array $ans$ of length $n$, initially each element is $-1$.

Next, we first check whether $k$ is greater than the length $n$ of the array nums. If it is, we directly return the answer array.

Otherwise, we calculate the sum $s$ of the first $k$ elements of the array nums, and assign the quotient of $s$ divided by $k$ to the $j$-th element of the answer array $ans$, where $j = k / 2$.

Then, we start traversing the array nums from $k$. For each iteration, we add the value of $nums[i]$ to $s$ and subtract the value of $nums[i - k]$, and update $j = j + 1$. Then we get the sum $s$ of the subarray with the $j$-th element as the center and radius $k$, and assign the quotient of $s$ divided by $k$ to the $j$-th element of the answer array $ans$.

Finally, we return the answer array.

The time complexity is $O(n)$, where $n$ is the length of the array nums. Ignoring the space consumption of the answer, the space complexity is $O(1)$.

Python3JavaC++GoTypeScript

class Solution:
    def getAverages(self, nums: List[int], k: int) -> List[int]:
        k = k << 1 | 1
        n = len(nums)
        ans = [-1] * n
        if k > n:
            return ans
        s = sum(nums[:k])
        j = k // 2
        ans[j] = s // k
        for i in range(k, n):
            j += 1
            s += nums[i] - nums[i - k]
            ans[j] = s // k
        return ans

class Solution {
    public int[] getAverages(int[] nums, int k) {
        k = k << 1 | 1;
        int n = nums.length;
        int[] ans = new int[n];
        Arrays.fill(ans, -1);
        if (k > n) {
            return ans;
        }
        long s = 0;
        for (int i = 0; i < k; ++i) {
            s += nums[i];
        }
        int j = k / 2;
        ans[j] = (int) (s / k);
        for (int i = k; i < n; ++i) {
            s += nums[i] - nums[i - k];
            ans[++j] = (int) (s / k);
        }
        return ans;
    }
}

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {
        k = k << 1 | 1;
        int n = nums.size();
        vector<int> ans(n, -1);
        if (k > n) {
            return ans;
        }
        long long s = accumulate(nums.begin(), nums.begin() + k, 0LL);
        int j = k / 2;
        ans[j] = s / k;
        for (int i = k; i < n; ++i) {
            s += nums[i] - nums[i - k];
            ans[++j] = s / k;
        }
        return ans;
    }
};

func getAverages(nums []int, k int) []int {
    k = k<<1 | 1
    n := len(nums)
    ans := make([]int, n)
    for i := range ans {
        ans[i] = -1
    }
    if k > n {
        return ans
    }
    s := 0
    for _, x := range nums[:k] {
        s += x
    }
    j := k >> 1
    ans[j] = s / k
    for i := k; i < n; i++ {
        s += nums[i] - nums[i-k]
        j++
        ans[j] = s / k
    }
    return ans
}

function getAverages(nums: number[], k: number): number[] {
    k = (k << 1) | 1;
    const n = nums.length;
    const ans: number[] = Array(n).fill(-1);
    if (k > n) {
        return ans;
    }
    let s = nums.slice(0, k).reduce((acc, cur) => acc + cur, 0);
    let j = k >> 1;
    ans[j] = Math.floor(s / k);
    for (let i = k; i < n; ++i) {
        s += nums[i] - nums[i - k];
        ans[++j] = Math.floor(s / k);
    }
    return ans;
}

Solution 2: Another Way of Sliding Window

We maintain a window of size $k \times 2 + 1$, and let the sum of all elements in the window be $s$.

Like Solution 1, we create an answer array $ans$ of length $n$, initially each element is $-1$.

Next, we traverse the array nums, add the value of $nums[i]$ to the sum $s$. If $i \geq k \times 2$, it means the window size is $k \times 2 + 1$ now, so we set $ans[i-k] = \frac{s}{k \times 2 + 1}$, then we subtract the value of $nums[i - k \times 2]$ from the sum $s$. Continue to the next element.