Depth-First Search
Breadth-First Search
Union Find
Array
Binary Search
Matrix
Heap (Priority Queue)
Description
Given an m x n integer matrix grid, return the maximum score of a path starting at (0, 0) and ending at (m - 1, n - 1) moving in the 4 cardinal directions.
The score of a path is the minimum value in that path.
For example, the score of the path 8 → 4 → 5 → 9 is 4.
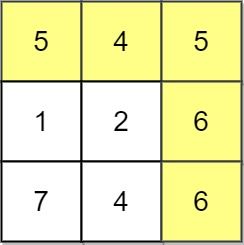
Example 1:
Input: grid = [[5,4,5],[1,2,6],[7,4,6]]
Output: 4
Explanation: The path with the maximum score is highlighted in yellow.
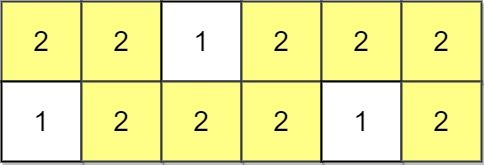
Example 2:
Input: grid = [[2,2,1,2,2,2],[1,2,2,2,1,2]]
Output: 2
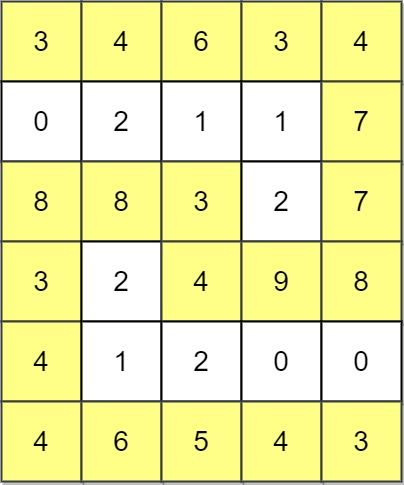
Example 3:
Input: grid = [[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]]
Output: 3
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1000 <= grid[i][j] <= 109
Solutions
Solution 1: Sorting + Union-Find
First, we construct a triplet $(v, i, j)$ for each element in the matrix, where $v$ represents the element value, and $i$ and $j$ represent the row and column of the element in the matrix, respectively. Then we sort these triplets in descending order by element value and store them in a list $q$.
Next, we take out the triplets from $q$ in order, use the corresponding element value as the score of the path, and mark the position as visited. Then we check the four adjacent positions (up, down, left, and right) of this position. If an adjacent position has been visited, we merge this position with the current position. If we find that the position $(0, 0)$ and the position $(m - 1, n - 1)$ have been merged, we can directly return the score of the current path as the answer.
The time complexity is $O(m \times n \times (\log (m \times n) + \alpha(m \times n)))$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively.
Python3 Java C++ Go TypeScript Rust
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 class Solution :
def maximumMinimumPath ( self , grid : List [ List [ int ]]) -> int :
def find ( x : int ) -> int :
if p [ x ] != x :
p [ x ] = find ( p [ x ])
return p [ x ]
m , n = len ( grid ), len ( grid [ 0 ])
p = list ( range ( m * n ))
q = [( v , i , j ) for i , row in enumerate ( grid ) for j , v in enumerate ( row )]
q . sort ()
ans = 0
dirs = ( - 1 , 0 , 1 , 0 , - 1 )
vis = set ()
while find ( 0 ) != find ( m * n - 1 ):
v , i , j = q . pop ()
ans = v
vis . add (( i , j ))
for a , b in pairwise ( dirs ):
x , y = i + a , j + b
if ( x , y ) in vis :
p [ find ( i * n + j )] = find ( x * n + y )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 class Solution {
private int [] p ;
public int maximumMinimumPath ( int [][] grid ) {
int m = grid . length , n = grid [ 0 ] . length ;
p = new int [ m * n ] ;
List < int []> q = new ArrayList <> ();
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
q . add ( new int [] { grid [ i ][ j ] , i , j });
p [ i * n + j ] = i * n + j ;
}
}
q . sort (( a , b ) -> b [ 0 ] - a [ 0 ] );
boolean [][] vis = new boolean [ m ][ n ] ;
int [] dirs = { - 1 , 0 , 1 , 0 , - 1 };
int ans = 0 ;
for ( int i = 0 ; find ( 0 ) != find ( m * n - 1 ); ++ i ) {
int [] t = q . get ( i );
vis [ t [ 1 ]][ t [ 2 ]] = true ;
ans = t [ 0 ] ;
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = t [ 1 ] + dirs [ k ] , y = t [ 2 ] + dirs [ k + 1 ] ;
if ( x >= 0 && x < m && y >= 0 && y < n && vis [ x ][ y ] ) {
p [ find ( x * n + y ) ] = find ( t [ 1 ] * n + t [ 2 ] );
}
}
}
return ans ;
}
private int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ] );
}
return p [ x ] ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 class Solution {
public :
int maximumMinimumPath ( vector < vector < int >>& grid ) {
int m = grid . size (), n = grid [ 0 ]. size ();
vector < tuple < int , int , int >> q ;
vector < int > p ( m * n );
iota ( p . begin (), p . end (), 0 );
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
q . emplace_back ( grid [ i ][ j ], i , j );
}
}
function < int ( int ) > find = [ & ]( int x ) {
return p [ x ] == x ? x : p [ x ] = find ( p [ x ]);
};
sort ( q . begin (), q . end (), greater < tuple < int , int , int >> ());
int ans = 0 ;
int dirs [ 5 ] = { -1 , 0 , 1 , 0 , -1 };
bool vis [ m ][ n ];
memset ( vis , false , sizeof ( vis ));
for ( auto & [ v , i , j ] : q ) {
vis [ i ][ j ] = true ;
ans = v ;
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i + dirs [ k ], y = j + dirs [ k + 1 ];
if ( x >= 0 && x < m && y >= 0 && y < n && vis [ x ][ y ]) {
p [ find ( x * n + y )] = find ( i * n + j );
}
}
if ( find ( 0 ) == find ( m * n - 1 )) {
break ;
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 func maximumMinimumPath ( grid [][] int ) ( ans int ) {
m , n := len ( grid ), len ( grid [ 0 ])
p := make ([] int , m * n )
vis := make ([][] bool , m )
q := [][ 3 ] int {}
for i , row := range grid {
vis [ i ] = make ([] bool , n )
for j , v := range row {
p [ i * n + j ] = i * n + j
q = append ( q , [ 3 ] int { v , i , j })
}
}
sort . Slice ( q , func ( i , j int ) bool { return q [ i ][ 0 ] > q [ j ][ 0 ] })
var find func ( int ) int
find = func ( x int ) int {
if p [ x ] != x {
p [ x ] = find ( p [ x ])
}
return p [ x ]
}
dirs := [ 5 ] int { - 1 , 0 , 1 , 0 , - 1 }
for _ , t := range q {
v , i , j := t [ 0 ], t [ 1 ], t [ 2 ]
ans = v
vis [ i ][ j ] = true
for k := 0 ; k < 4 ; k ++ {
x , y := i + dirs [ k ], j + dirs [ k + 1 ]
if 0 <= x && x < m && 0 <= y && y < n && vis [ x ][ y ] {
p [ find ( x * n + y )] = find ( i * n + j )
}
}
if find ( 0 ) == find ( m * n - 1 ) {
break
}
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 function maximumMinimumPath ( grid : number [][]) : number {
const m = grid . length ;
const n = grid [ 0 ]. length ;
const p : number [] = Array ( m * n )
. fill ( 0 )
. map (( _ , i ) => i );
const q : number [][] = [];
for ( let i = 0 ; i < m ; ++ i ) {
for ( let j = 0 ; j < n ; ++ j ) {
q . push ([ grid [ i ][ j ], i , j ]);
}
}
q . sort (( a , b ) => b [ 0 ] - a [ 0 ]);
const find = ( x : number ) : number => {
if ( p [ x ] !== x ) {
p [ x ] = find ( p [ x ]);
}
return p [ x ];
};
const dirs : number [] = [ - 1 , 0 , 1 , 0 , - 1 ];
const vis : boolean [][] = Array ( m )
. fill ( 0 )
. map (() => Array ( n ). fill ( false ));
let ans = 0 ;
for ( let k = 0 ; find ( 0 ) !== find ( m * n - 1 ); ++ k ) {
const [ t , i , j ] = q [ k ];
ans = t ;
vis [ i ][ j ] = true ;
for ( let d = 0 ; d < 4 ; ++ d ) {
const [ x , y ] = [ i + dirs [ d ], j + dirs [ d + 1 ]];
if ( x >= 0 && x < m && y >= 0 && y < n && vis [ x ][ y ]) {
p [ find ( i * n + j )] = find ( x * n + y );
}
}
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77 struct UnionFind {
p : Vec < usize > ,
size : Vec < usize > ,
}
impl UnionFind {
fn new ( n : usize ) -> Self {
let p : Vec < usize > = ( 0 .. n ). collect ();
let size = vec! [ 1 ; n ];
UnionFind { p , size }
}
fn find ( & mut self , x : usize ) -> usize {
if self . p [ x ] != x {
self . p [ x ] = self . find ( self . p [ x ]);
}
self . p [ x ]
}
fn union ( & mut self , a : usize , b : usize ) {
let pa = self . find ( a );
let pb = self . find ( b );
if pa != pb {
if self . size [ pa ] > self . size [ pb ] {
self . p [ pb ] = pa ;
self . size [ pa ] += self . size [ pb ];
} else {
self . p [ pa ] = pb ;
self . size [ pb ] += self . size [ pa ];
}
}
}
}
impl Solution {
pub fn maximum_minimum_path ( grid : Vec < Vec < i32 >> ) -> i32 {
let m = grid . len ();
let n = grid [ 0 ]. len ();
let mut uf = UnionFind :: new ( m * n );
let mut q : Vec < Vec < i32 >> = Vec :: new ();
for i in 0 .. m {
for j in 0 .. n {
q . push ( vec! [ grid [ i ][ j ], i as i32 , j as i32 ]);
}
}
q . sort_by ( | a , b | b [ 0 ]. cmp ( & a [ 0 ]));
let mut vis : Vec < Vec < bool >> = vec! [ vec! [ false ; n ]; m ];
let dirs : [ i32 ; 5 ] = [ - 1 , 0 , 1 , 0 , - 1 ];
let mut ans = 0 ;
for k in 0 .. q . len () {
if uf . find ( 0 ) == uf . find ( m * n - 1 ) {
break ;
}
let t = & q [ k ];
let ( v , i , j ) = ( t [ 0 ], t [ 1 ] as usize , t [ 2 ] as usize );
ans = v ;
vis [ i ][ j ] = true ;
for d in 0 .. 4 {
let x = ( i as i32 ) + dirs [ d ];
let y = ( j as i32 ) + dirs [ d + 1 ];
if
x >= 0 &&
x < ( m as i32 ) &&
y >= 0 &&
y < ( n as i32 ) &&
vis [ x as usize ][ y as usize ]
{
uf . union (( x as usize ) * n + ( y as usize ), i * n + j );
}
}
}
ans
}
}
Solution 2
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 class UnionFind :
__slots__ = ( "p" , "size" )
def __init__ ( self , n ):
self . p = list ( range ( n ))
self . size = [ 1 ] * n
def find ( self , x : int ) -> int :
if self . p [ x ] != x :
self . p [ x ] = self . find ( self . p [ x ])
return self . p [ x ]
def union ( self , a : int , b : int ) -> bool :
pa , pb = self . find ( a ), self . find ( b )
if pa == pb :
return False
if self . size [ pa ] > self . size [ pb ]:
self . p [ pb ] = pa
self . size [ pa ] += self . size [ pb ]
else :
self . p [ pa ] = pb
self . size [ pb ] += self . size [ pa ]
return True
class Solution :
def maximumMinimumPath ( self , grid : List [ List [ int ]]) -> int :
m , n = len ( grid ), len ( grid [ 0 ])
uf = UnionFind ( m * n )
q = [( v , i , j ) for i , row in enumerate ( grid ) for j , v in enumerate ( row )]
q . sort ()
ans = 0
vis = set ()
dirs = ( - 1 , 0 , 1 , 0 , - 1 )
while uf . find ( 0 ) != uf . find ( m * n - 1 ):
v , i , j = q . pop ()
ans = v
vis . add (( i , j ))
for a , b in pairwise ( dirs ):
x , y = i + a , j + b
if ( x , y ) in vis :
uf . union ( x * n + y , i * n + j )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62 class UnionFind {
private int [] p ;
private int [] size ;
public UnionFind ( int n ) {
p = new int [ n ] ;
size = new int [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
p [ i ] = i ;
size [ i ] = 1 ;
}
}
public int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ] );
}
return p [ x ] ;
}
public void union ( int a , int b ) {
int pa = find ( a ), pb = find ( b );
if ( pa != pb ) {
if ( size [ pa ] > size [ pb ] ) {
p [ pb ] = pa ;
size [ pa ] += size [ pb ] ;
} else {
p [ pa ] = pb ;
size [ pb ] += size [ pa ] ;
}
}
}
}
class Solution {
public int maximumMinimumPath ( int [][] grid ) {
int m = grid . length , n = grid [ 0 ] . length ;
UnionFind uf = new UnionFind ( m * n );
List < int []> q = new ArrayList <> ();
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
q . add ( new int [] { grid [ i ][ j ] , i , j });
}
}
q . sort (( a , b ) -> b [ 0 ] - a [ 0 ] );
boolean [][] vis = new boolean [ m ][ n ] ;
int [] dirs = { - 1 , 0 , 1 , 0 , - 1 };
int ans = 0 ;
for ( int i = 0 ; uf . find ( 0 ) != uf . find ( m * n - 1 ); ++ i ) {
int [] t = q . get ( i );
vis [ t [ 1 ]][ t [ 2 ]] = true ;
ans = t [ 0 ] ;
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = t [ 1 ] + dirs [ k ] , y = t [ 2 ] + dirs [ k + 1 ] ;
if ( x >= 0 && x < m && y >= 0 && y < n && vis [ x ][ y ] ) {
uf . union ( x * n + y , t [ 1 ] * n + t [ 2 ] );
}
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64 class UnionFind {
public :
UnionFind ( int n ) {
p = vector < int > ( n );
size = vector < int > ( n , 1 );
iota ( p . begin (), p . end (), 0 );
}
void unite ( int a , int b ) {
int pa = find ( a ), pb = find ( b );
if ( pa != pb ) {
if ( size [ pa ] > size [ pb ]) {
p [ pb ] = pa ;
size [ pa ] += size [ pb ];
} else {
p [ pa ] = pb ;
size [ pb ] += size [ pa ];
}
}
}
int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ]);
}
return p [ x ];
}
private :
vector < int > p , size ;
};
class Solution {
public :
int maximumMinimumPath ( vector < vector < int >>& grid ) {
int m = grid . size (), n = grid [ 0 ]. size ();
vector < tuple < int , int , int >> q ;
UnionFind uf ( m * n );
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
q . emplace_back ( grid [ i ][ j ], i , j );
}
}
sort ( q . begin (), q . end (), greater < tuple < int , int , int >> ());
int ans = 0 ;
int dirs [ 5 ] = { -1 , 0 , 1 , 0 , -1 };
bool vis [ m ][ n ];
memset ( vis , false , sizeof ( vis ));
for ( auto & [ v , i , j ] : q ) {
vis [ i ][ j ] = true ;
ans = v ;
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i + dirs [ k ], y = j + dirs [ k + 1 ];
if ( x >= 0 && x < m && y >= 0 && y < n && vis [ x ][ y ]) {
uf . unite ( x * n + y , i * n + j );
}
}
if ( uf . find ( 0 ) == uf . find ( m * n - 1 )) {
break ;
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63 type unionFind struct {
p , size [] int
}
func newUnionFind ( n int ) * unionFind {
p := make ([] int , n )
size := make ([] int , n )
for i := range p {
p [ i ] = i
size [ i ] = 1
}
return & unionFind { p , size }
}
func ( uf * unionFind ) find ( x int ) int {
if uf . p [ x ] != x {
uf . p [ x ] = uf . find ( uf . p [ x ])
}
return uf . p [ x ]
}
func ( uf * unionFind ) union ( a , b int ) {
pa , pb := uf . find ( a ), uf . find ( b )
if pa != pb {
if uf . size [ pa ] > uf . size [ pb ] {
uf . p [ pb ] = pa
uf . size [ pa ] += uf . size [ pb ]
} else {
uf . p [ pa ] = pb
uf . size [ pb ] += uf . size [ pa ]
}
}
}
func maximumMinimumPath ( grid [][] int ) ( ans int ) {
m , n := len ( grid ), len ( grid [ 0 ])
uf := newUnionFind ( m * n )
vis := make ([][] bool , m )
q := [][ 3 ] int {}
for i , row := range grid {
vis [ i ] = make ([] bool , n )
for j , v := range row {
q = append ( q , [ 3 ] int { v , i , j })
}
}
sort . Slice ( q , func ( i , j int ) bool { return q [ i ][ 0 ] > q [ j ][ 0 ] })
dirs := [ 5 ] int { - 1 , 0 , 1 , 0 , - 1 }
for _ , t := range q {
v , i , j := t [ 0 ], t [ 1 ], t [ 2 ]
ans = v
vis [ i ][ j ] = true
for k := 0 ; k < 4 ; k ++ {
x , y := i + dirs [ k ], j + dirs [ k + 1 ]
if 0 <= x && x < m && 0 <= y && y < n && vis [ x ][ y ] {
uf . union ( x * n + y , i * n + j )
}
}
if uf . find ( 0 ) == uf . find ( m * n - 1 ) {
break
}
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64 class UnionFind {
private p : number [];
private size : number [];
constructor ( n : number ) {
this . p = Array ( n )
. fill ( 0 )
. map (( _ , i ) => i );
this . size = Array ( n ). fill ( 1 );
}
find ( x : number ) : number {
if ( this . p [ x ] !== x ) {
this . p [ x ] = this . find ( this . p [ x ]);
}
return this . p [ x ];
}
union ( a : number , b : number ) : boolean {
const pa = this . find ( a );
const pb = this . find ( b );
if ( pa === pb ) {
return false ;
}
if ( this . size [ pa ] > this . size [ pb ]) {
this . p [ pb ] = pa ;
this . size [ pa ] += this . size [ pb ];
} else {
this . p [ pa ] = pb ;
this . size [ pb ] += this . size [ pa ];
}
return true ;
}
}
function maximumMinimumPath ( grid : number [][]) : number {
const m = grid . length ;
const n = grid [ 0 ]. length ;
const q : number [][] = [];
for ( let i = 0 ; i < m ; ++ i ) {
for ( let j = 0 ; j < n ; ++ j ) {
q . push ([ grid [ i ][ j ], i , j ]);
}
}
q . sort (( a , b ) => b [ 0 ] - a [ 0 ]);
const dirs : number [] = [ - 1 , 0 , 1 , 0 , - 1 ];
const vis : boolean [][] = Array ( m )
. fill ( 0 )
. map (() => Array ( n ). fill ( false ));
let ans = 0 ;
const uf = new UnionFind ( m * n );
for ( let k = 0 ; uf . find ( 0 ) !== uf . find ( m * n - 1 ); ++ k ) {
const [ t , i , j ] = q [ k ];
ans = t ;
vis [ i ][ j ] = true ;
for ( let d = 0 ; d < 4 ; ++ d ) {
const [ x , y ] = [ i + dirs [ d ], j + dirs [ d + 1 ]];
if ( x >= 0 && x < m && y >= 0 && y < n && vis [ x ][ y ]) {
uf . union ( i * n + j , x * n + y );
}
}
}
return ans ;
}
GitHub