Depth-First Search
Breadth-First Search
Array
Matrix
Description
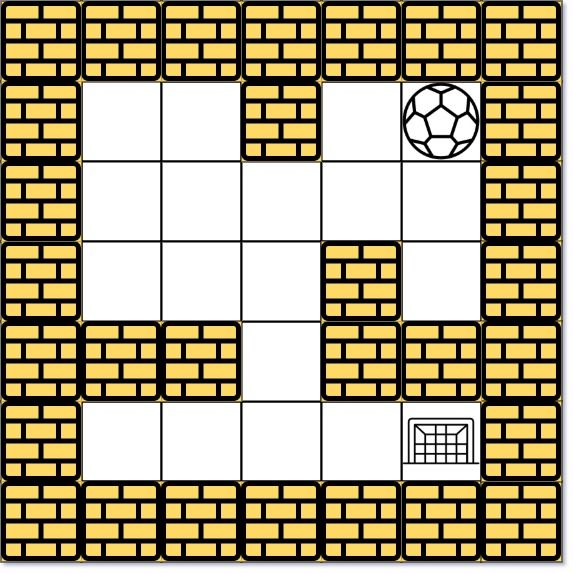
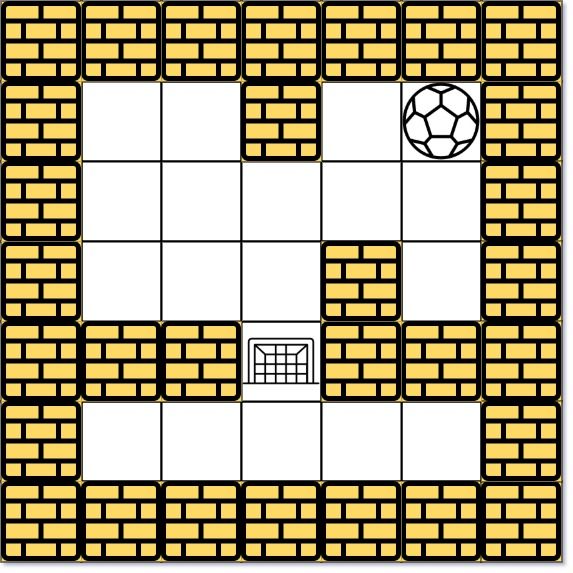
There is a ball in a maze with empty spaces (represented as 0) and walls (represented as 1). The ball can go through the empty spaces by rolling up, down, left or right , but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.
Given the m x n maze, the ball's start position and the destination, where start = [startrow , startcol ] and destination = [destinationrow , destinationcol ], return true if the ball can stop at the destination, otherwise return false.
You may assume that the borders of the maze are all walls (see examples).
Example 1:
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4]
Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.
Example 2:
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2]
Output: false
Explanation: There is no way for the ball to stop at the destination. Notice that you can pass through the destination but you cannot stop there.
Example 3:
Input: maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1]
Output: false
Constraints:
m == maze.lengthn == maze[i].length1 <= m, n <= 100maze[i][j] is 0 or 1.start.length == 2destination.length == 20 <= startrow , destinationrow <= m0 <= startcol , destinationcol <= nBoth the ball and the destination exist in an empty space, and they will not be in the same position initially.
The maze contains at least 2 empty spaces .
Solutions
Solution 1
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 class Solution :
def hasPath (
self , maze : List [ List [ int ]], start : List [ int ], destination : List [ int ]
) -> bool :
def dfs ( i , j ):
if vis [ i ][ j ]:
return
vis [ i ][ j ] = True
if [ i , j ] == destination :
return
for a , b in [[ 0 , - 1 ], [ 0 , 1 ], [ 1 , 0 ], [ - 1 , 0 ]]:
x , y = i , j
while 0 <= x + a < m and 0 <= y + b < n and maze [ x + a ][ y + b ] == 0 :
x , y = x + a , y + b
dfs ( x , y )
m , n = len ( maze ), len ( maze [ 0 ])
vis = [[ False ] * n for _ in range ( m )]
dfs ( start [ 0 ], start [ 1 ])
return vis [ destination [ 0 ]][ destination [ 1 ]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 class Solution {
private boolean [][] vis ;
private int [][] maze ;
private int [] d ;
private int m ;
private int n ;
public boolean hasPath ( int [][] maze , int [] start , int [] destination ) {
m = maze . length ;
n = maze [ 0 ] . length ;
d = destination ;
this . maze = maze ;
vis = new boolean [ m ][ n ] ;
dfs ( start [ 0 ] , start [ 1 ] );
return vis [ d [ 0 ]][ d [ 1 ]] ;
}
private void dfs ( int i , int j ) {
if ( vis [ i ][ j ] ) {
return ;
}
vis [ i ][ j ] = true ;
if ( i == d [ 0 ] && j == d [ 1 ] ) {
return ;
}
int [] dirs = { - 1 , 0 , 1 , 0 , - 1 };
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i , y = j ;
int a = dirs [ k ] , b = dirs [ k + 1 ] ;
while ( x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze [ x + a ][ y + b ] == 0 ) {
x += a ;
y += b ;
}
dfs ( x , y );
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 class Solution {
public :
vector < vector < int >> maze ;
vector < vector < bool >> vis ;
vector < int > d ;
int m ;
int n ;
bool hasPath ( vector < vector < int >>& maze , vector < int >& start , vector < int >& destination ) {
m = maze . size ();
n = maze [ 0 ]. size ();
d = destination ;
vis . resize ( m , vector < bool > ( n , false ));
this -> maze = maze ;
dfs ( start [ 0 ], start [ 1 ]);
return vis [ d [ 0 ]][ d [ 1 ]];
}
void dfs ( int i , int j ) {
if ( vis [ i ][ j ]) return ;
vis [ i ][ j ] = true ;
if ( i == d [ 0 ] && j == d [ 1 ]) return ;
vector < int > dirs = { -1 , 0 , 1 , 0 , -1 };
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i , y = j ;
int a = dirs [ k ], b = dirs [ k + 1 ];
while ( x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze [ x + a ][ y + b ] == 0 ) {
x += a ;
y += b ;
}
dfs ( x , y );
}
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 func hasPath ( maze [][] int , start [] int , destination [] int ) bool {
m , n := len ( maze ), len ( maze [ 0 ])
vis := make ([][] bool , m )
for i := range vis {
vis [ i ] = make ([] bool , n )
}
var dfs func ( i , j int )
dfs = func ( i , j int ) {
if vis [ i ][ j ] {
return
}
vis [ i ][ j ] = true
if i == destination [ 0 ] && j == destination [ 1 ] {
return
}
dirs := [] int { - 1 , 0 , 1 , 0 , - 1 }
for k := 0 ; k < 4 ; k ++ {
x , y := i , j
a , b := dirs [ k ], dirs [ k + 1 ]
for x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze [ x + a ][ y + b ] == 0 {
x += a
y += b
}
dfs ( x , y )
}
}
dfs ( start [ 0 ], start [ 1 ])
return vis [ destination [ 0 ]][ destination [ 1 ]]
}
Solution 2
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 class Solution :
def hasPath (
self , maze : List [ List [ int ]], start : List [ int ], destination : List [ int ]
) -> bool :
m , n = len ( maze ), len ( maze [ 0 ])
q = deque ([ start ])
rs , cs = start
vis = {( rs , cs )}
while q :
i , j = q . popleft ()
for a , b in [[ 0 , - 1 ], [ 0 , 1 ], [ - 1 , 0 ], [ 1 , 0 ]]:
x , y = i , j
while 0 <= x + a < m and 0 <= y + b < n and maze [ x + a ][ y + b ] == 0 :
x , y = x + a , y + b
if [ x , y ] == destination :
return True
if ( x , y ) not in vis :
vis . add (( x , y ))
q . append (( x , y ))
return False
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 class Solution {
public boolean hasPath ( int [][] maze , int [] start , int [] destination ) {
int m = maze . length ;
int n = maze [ 0 ] . length ;
boolean [][] vis = new boolean [ m ][ n ] ;
vis [ start [ 0 ]][ start [ 1 ]] = true ;
Deque < int []> q = new LinkedList <> ();
q . offer ( start );
int [] dirs = { - 1 , 0 , 1 , 0 , - 1 };
while ( ! q . isEmpty ()) {
int [] p = q . poll ();
int i = p [ 0 ] , j = p [ 1 ] ;
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i , y = j ;
int a = dirs [ k ] , b = dirs [ k + 1 ] ;
while (
x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze [ x + a ][ y + b ] == 0 ) {
x += a ;
y += b ;
}
if ( x == destination [ 0 ] && y == destination [ 1 ] ) {
return true ;
}
if ( ! vis [ x ][ y ] ) {
vis [ x ][ y ] = true ;
q . offer ( new int [] { x , y });
}
}
}
return false ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 class Solution {
public :
bool hasPath ( vector < vector < int >>& maze , vector < int >& start , vector < int >& destination ) {
int m = maze . size ();
int n = maze [ 0 ]. size ();
queue < vector < int >> q {{ start }};
vector < vector < bool >> vis ( m , vector < bool > ( n ));
vis [ start [ 0 ]][ start [ 1 ]] = true ;
vector < int > dirs = { -1 , 0 , 1 , 0 , -1 };
while ( ! q . empty ()) {
auto p = q . front ();
q . pop ();
int i = p [ 0 ], j = p [ 1 ];
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i , y = j ;
int a = dirs [ k ], b = dirs [ k + 1 ];
while ( x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze [ x + a ][ y + b ] == 0 ) {
x += a ;
y += b ;
}
if ( x == destination [ 0 ] && y == destination [ 1 ]) return 1 ;
if ( ! vis [ x ][ y ]) {
vis [ x ][ y ] = true ;
q . push ({ x , y });
}
}
}
return 0 ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 func hasPath ( maze [][] int , start [] int , destination [] int ) bool {
m , n := len ( maze ), len ( maze [ 0 ])
vis := make ([][] bool , m )
for i := range vis {
vis [ i ] = make ([] bool , n )
}
vis [ start [ 0 ]][ start [ 1 ]] = true
q := [][] int { start }
dirs := [] int { - 1 , 0 , 1 , 0 , - 1 }
for len ( q ) > 0 {
i , j := q [ 0 ][ 0 ], q [ 0 ][ 1 ]
q = q [ 1 :]
for k := 0 ; k < 4 ; k ++ {
x , y := i , j
a , b := dirs [ k ], dirs [ k + 1 ]
for x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze [ x + a ][ y + b ] == 0 {
x += a
y += b
}
if x == destination [ 0 ] && y == destination [ 1 ] {
return true
}
if ! vis [ x ][ y ] {
vis [ x ][ y ] = true
q = append ( q , [] int { x , y })
}
}
}
return false
}
GitHub