Skip to content

694. Number of Distinct Islands πŸ”’

Description

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

An island is considered to be the same as another if and only if one island can be translated (and not rotated or reflected) to equal the other.

Return the number of distinct islands.

 

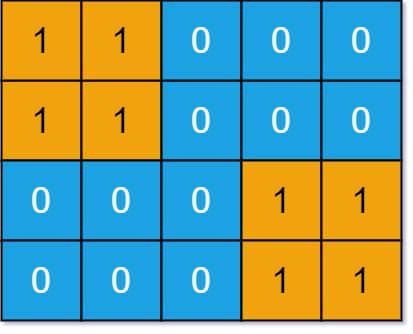
Example 1:

Input: grid = [[1,1,0,0,0],[1,1,0,0,0],[0,0,0,1,1],[0,0,0,1,1]]
Output: 1

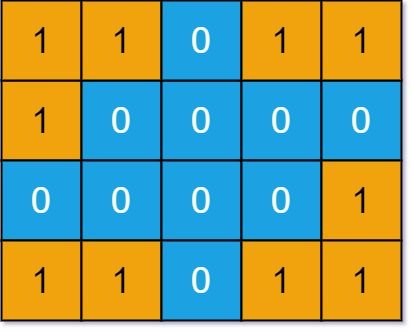
Example 2:

Input: grid = [[1,1,0,1,1],[1,0,0,0,0],[0,0,0,0,1],[1,1,0,1,1]]
Output: 3

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 50
  • grid[i][j] is either 0 or 1.

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def numDistinctIslands(self, grid: List[List[int]]) -> int:
        def dfs(i: int, j: int, k: int):
            grid[i][j] = 0
            path.append(str(k))
            dirs = (-1, 0, 1, 0, -1)
            for h in range(1, 5):
                x, y = i + dirs[h - 1], j + dirs[h]
                if 0 <= x < m and 0 <= y < n and grid[x][y]:
                    dfs(x, y, h)
            path.append(str(-k))

        paths = set()
        path = []
        m, n = len(grid), len(grid[0])
        for i, row in enumerate(grid):
            for j, x in enumerate(row):
                if x:
                    dfs(i, j, 0)
                    paths.add("".join(path))
                    path.clear()
        return len(paths)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    private int m;
    private int n;
    private int[][] grid;
    private StringBuilder path = new StringBuilder();

    public int numDistinctIslands(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        this.grid = grid;
        Set<String> paths = new HashSet<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    dfs(i, j, 0);
                    paths.add(path.toString());
                    path.setLength(0);
                }
            }
        }
        return paths.size();
    }

    private void dfs(int i, int j, int k) {
        grid[i][j] = 0;
        path.append(k);
        int[] dirs = {-1, 0, 1, 0, -1};
        for (int h = 1; h < 5; ++h) {
            int x = i + dirs[h - 1];
            int y = j + dirs[h];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                dfs(x, y, h);
            }
        }
        path.append(k);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int numDistinctIslands(vector<vector<int>>& grid) {
        unordered_set<string> paths;
        string path;
        int m = grid.size(), n = grid[0].size();
        int dirs[5] = {-1, 0, 1, 0, -1};

        function<void(int, int, int)> dfs = [&](int i, int j, int k) {
            grid[i][j] = 0;
            path += to_string(k);
            for (int h = 1; h < 5; ++h) {
                int x = i + dirs[h - 1], y = j + dirs[h];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y]) {
                    dfs(x, y, h);
                }
            }
            path += to_string(k);
        };

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j]) {
                    dfs(i, j, 0);
                    paths.insert(path);
                    path.clear();
                }
            }
        }
        return paths.size();
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func numDistinctIslands(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    paths := map[string]bool{}
    path := []byte{}
    dirs := [5]int{-1, 0, 1, 0, -1}
    var dfs func(i, j, k int)
    dfs = func(i, j, k int) {
        grid[i][j] = 0
        path = append(path, byte(k))
        for h := 1; h < 5; h++ {
            x, y := i+dirs[h-1], j+dirs[h]
            if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 {
                dfs(x, y, h)
            }
        }
        path = append(path, byte(k))
    }
    for i, row := range grid {
        for j, x := range row {
            if x == 1 {
                dfs(i, j, 0)
                paths[string(path)] = true
                path = path[:0]
            }
        }
    }
    return len(paths)
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
function numDistinctIslands(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const paths: Set<string> = new Set();
    const path: number[] = [];
    const dirs: number[] = [-1, 0, 1, 0, -1];
    const dfs = (i: number, j: number, k: number) => {
        grid[i][j] = 0;
        path.push(k);
        for (let h = 1; h < 5; ++h) {
            const [x, y] = [i + dirs[h - 1], j + dirs[h]];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y]) {
                dfs(x, y, h);
            }
        }
        path.push(k);
    };
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j]) {
                dfs(i, j, 0);
                paths.add(path.join(','));
                path.length = 0;
            }
        }
    }
    return paths.size;
}

Comments