2658. Maximum Number of Fish in a Grid

Description

You are given a 0-indexed 2D matrix grid of size m x n, where (r, c) represents:

A land cell if grid[r][c] = 0, or
A water cell containing grid[r][c] fish, if grid[r][c] > 0.

A fisher can start at any water cell (r, c) and can do the following operations any number of times:

Catch all the fish at cell (r, c), or
Move to any adjacent water cell.

Return the maximum number of fish the fisher can catch if he chooses his starting cell optimally, or 0 if no water cell exists.

An adjacent cell of the cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) or (r - 1, c) if it exists.

Example 1:

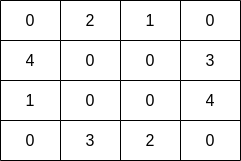
Input: grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]]
Output: 7
Explanation: The fisher can start at cell (1,3) and collect 3 fish, then move to cell (2,3) and collect 4 fish.

Example 2:

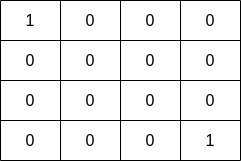
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]]
Output: 1
Explanation: The fisher can start at cells (0,0) or (3,3) and collect a single fish.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 10
0 <= grid[i][j] <= 10

Solutions

Solution 1: DFS

According to the problem description, we only need to find the number of fish in each connected water area and then take the maximum value. Therefore, we can use the depth-first search method to solve this problem.

We define a function $dfs(i, j)$, which indicates the maximum number of fish that can be caught starting from the cell in the $i$-th row and the $j$-th column. The execution logic of the function $dfs(i, j)$ is as follows:

We use a variable $cnt$ to record the number of fish in the current cell, and then set the number of fish in the current cell to $0$, indicating that it has been fished. Then we traverse the four directions of the current cell, if the cell $(x, y)$ in a certain direction is in the grid and is a water cell, then we recursively call the $dfs(x, y)$ function and add the return value to $cnt$. Finally, return $cnt$.

In the main function, we traverse all the cells $(i, j)$. If the current cell is a water cell, we call the $dfs(i, j)$ function, take the maximum value of the return value as the answer, and return it.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. where $m$ and $n$ are the number of rows and columns of the grid graph respectively.

Python3JavaC++GoTypeScript

class Solution:
    def findMaxFish(self, grid: List[List[int]]) -> int:
        def dfs(i: int, j: int) -> int:
            cnt = grid[i][j]
            grid[i][j] = 0
            for a, b in pairwise((-1, 0, 1, 0, -1)):
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and grid[x][y]:
                    cnt += dfs(x, y)
            return cnt

        m, n = len(grid), len(grid[0])
        ans = 0
        for i in range(m):
            for j in range(n):
                if grid[i][j]:
                    ans = max(ans, dfs(i, j))
        return ans

class Solution {
    private int[][] grid;
    private int m;
    private int n;

    public int findMaxFish(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        this.grid = grid;
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] > 0) {
                    ans = Math.max(ans, dfs(i, j));
                }
            }
        }
        return ans;
    }

    private int dfs(int i, int j) {
        int cnt = grid[i][j];
        grid[i][j] = 0;
        int[] dirs = {-1, 0, 1, 0, -1};
        for (int k = 0; k < 4; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0) {
                cnt += dfs(x, y);
            }
        }
        return cnt;
    }
}

class Solution {
public:
    int findMaxFish(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int ans = 0;
        function<int(int, int)> dfs = [&](int i, int j) -> int {
            int cnt = grid[i][j];
            grid[i][j] = 0;
            int dirs[5] = {-1, 0, 1, 0, -1};
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y]) {
                    cnt += dfs(x, y);
                }
            }
            return cnt;
        };
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j]) {
                    ans = max(ans, dfs(i, j));
                }
            }
        }
        return ans;
    }
};

func findMaxFish(grid [][]int) (ans int) {
    m, n := len(grid), len(grid[0])
    dirs := [5]int{-1, 0, 1, 0, -1}
    var dfs func(i, j int) int
    dfs = func(i, j int) int {
        cnt := grid[i][j]
        grid[i][j] = 0
        for k := 0; k < 4; k++ {
            x, y := i+dirs[k], j+dirs[k+1]
            if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0 {
                cnt += dfs(x, y)
            }
        }
        return cnt
    }
    for i := range grid {
        for j := range grid[i] {
            if grid[i][j] > 0 {
                ans = max(ans, dfs(i, j))
            }
        }
    }
    return
}

function findMaxFish(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;

    const dirs = [-1, 0, 1, 0, -1];
    const dfs = (i: number, j: number): number => {
        let cnt = grid[i][j];
        grid[i][j] = 0;
        for (let k = 0; k < 4; ++k) {
            const x = i + dirs[k];
            const y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0) {
                cnt += dfs(x, y);
            }
        }
        return cnt;
    };

    let ans = 0;
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j] > 0) {
                ans = Math.max(ans, dfs(i, j));
            }
        }
    }
    return ans;
}

2658. Maximum Number of Fish in a Grid

Description

Solutions

Solution 1: DFS

Comments