Tree
Depth-First Search
Math
Dynamic Programming
Number Theory
Description
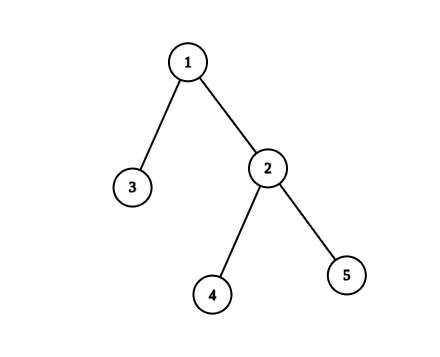
There is an undirected tree with n nodes labeled from 1 to n. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ui , vi ] indicates that there is an edge between nodes ui and vi in the tree.
Return the number of valid paths in the tree .
A path (a, b) is valid if there exists exactly one prime number among the node labels in the path from a to b.
Note that:
The path (a, b) is a sequence of distinct nodes starting with node a and ending with node b such that every two adjacent nodes in the sequence share an edge in the tree.
Path (a, b) and path (b, a) are considered the same and counted only once .
Example 1:
Input: n = 5, edges = [[1,2],[1,3],[2,4],[2,5]]
Output: 4
Explanation: The pairs with exactly one prime number on the path between them are:
- (1, 2) since the path from 1 to 2 contains prime number 2.
- (1, 3) since the path from 1 to 3 contains prime number 3.
- (1, 4) since the path from 1 to 4 contains prime number 2.
- (2, 4) since the path from 2 to 4 contains prime number 2.
It can be shown that there are only 4 valid paths.
Example 2:
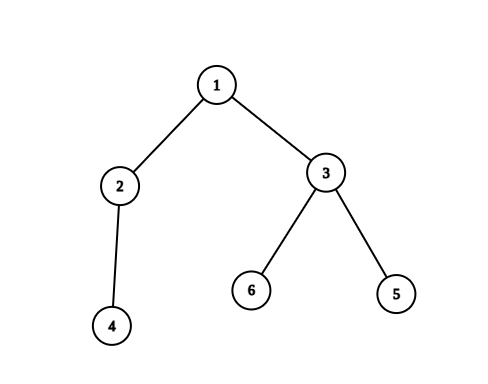
Input: n = 6, edges = [[1,2],[1,3],[2,4],[3,5],[3,6]]
Output: 6
Explanation: The pairs with exactly one prime number on the path between them are:
- (1, 2) since the path from 1 to 2 contains prime number 2.
- (1, 3) since the path from 1 to 3 contains prime number 3.
- (1, 4) since the path from 1 to 4 contains prime number 2.
- (1, 6) since the path from 1 to 6 contains prime number 3.
- (2, 4) since the path from 2 to 4 contains prime number 2.
- (3, 6) since the path from 3 to 6 contains prime number 3.
It can be shown that there are only 6 valid paths.
Constraints:
1 <= n <= 105 edges.length == n - 1edges[i].length == 21 <= ui , vi <= nThe input is generated such that edges represent a valid tree.
Solutions
Solution 1: Preprocessing + Union-Find + Enumeration
We can preprocess to get all the prime numbers in $[1, n]$, where $prime[i]$ indicates whether $i$ is a prime number.
Next, we build a graph $g$ based on the two-dimensional integer array, where $g[i]$ represents all the neighbor nodes of node $i$. If both nodes of an edge are not prime numbers, we merge these two nodes into the same connected component.
Then, we enumerate all prime numbers $i$ in the range of $[1, n]$, considering all paths that include $i$.
Since $i$ is already a prime number, if $i$ is an endpoint of the path, we only need to accumulate the sizes of all connected components adjacent to node $i$. If $i$ is a middle point on the path, we need to accumulate the product of the sizes of any two adjacent connected components.
The time complexity is $O(n \times \alpha(n))$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes, and $\alpha$ is the inverse function of the Ackermann function.
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53 class UnionFind :
def __init__ ( self , n ):
self . p = list ( range ( n ))
self . size = [ 1 ] * n
def find ( self , x ):
if self . p [ x ] != x :
self . p [ x ] = self . find ( self . p [ x ])
return self . p [ x ]
def union ( self , a , b ):
pa , pb = self . find ( a ), self . find ( b )
if pa == pb :
return False
if self . size [ pa ] > self . size [ pb ]:
self . p [ pb ] = pa
self . size [ pa ] += self . size [ pb ]
else :
self . p [ pa ] = pb
self . size [ pb ] += self . size [ pa ]
return True
mx = 10 ** 5 + 10
prime = [ True ] * ( mx + 1 )
prime [ 0 ] = prime [ 1 ] = False
for i in range ( 2 , mx + 1 ):
if prime [ i ]:
for j in range ( i * i , mx + 1 , i ):
prime [ j ] = False
class Solution :
def countPaths ( self , n : int , edges : List [ List [ int ]]) -> int :
g = [[] for _ in range ( n + 1 )]
uf = UnionFind ( n + 1 )
for u , v in edges :
g [ u ] . append ( v )
g [ v ] . append ( u )
if prime [ u ] + prime [ v ] == 0 :
uf . union ( u , v )
ans = 0
for i in range ( 1 , n + 1 ):
if prime [ i ]:
t = 0
for j in g [ i ]:
if not prime [ j ]:
cnt = uf . size [ uf . find ( j )]
ans += cnt
ans += t * cnt
t += cnt
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94 class PrimeTable {
private final boolean [] prime ;
public PrimeTable ( int n ) {
prime = new boolean [ n + 1 ] ;
Arrays . fill ( prime , true );
prime [ 0 ] = false ;
prime [ 1 ] = false ;
for ( int i = 2 ; i <= n ; ++ i ) {
if ( prime [ i ] ) {
for ( int j = i + i ; j <= n ; j += i ) {
prime [ j ] = false ;
}
}
}
}
public boolean isPrime ( int x ) {
return prime [ x ] ;
}
}
class UnionFind {
private final int [] p ;
private final int [] size ;
public UnionFind ( int n ) {
p = new int [ n ] ;
size = new int [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
p [ i ] = i ;
size [ i ] = 1 ;
}
}
public int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ] );
}
return p [ x ] ;
}
public boolean union ( int a , int b ) {
int pa = find ( a ), pb = find ( b );
if ( pa == pb ) {
return false ;
}
if ( size [ pa ] > size [ pb ] ) {
p [ pb ] = pa ;
size [ pa ] += size [ pb ] ;
} else {
p [ pa ] = pb ;
size [ pb ] += size [ pa ] ;
}
return true ;
}
public int size ( int x ) {
return size [ find ( x ) ] ;
}
}
class Solution {
private static final PrimeTable PT = new PrimeTable ( 100010 );
public long countPaths ( int n , int [][] edges ) {
List < Integer >[] g = new List [ n + 1 ] ;
Arrays . setAll ( g , i -> new ArrayList <> ());
UnionFind uf = new UnionFind ( n + 1 );
for ( int [] e : edges ) {
int u = e [ 0 ] , v = e [ 1 ] ;
g [ u ] . add ( v );
g [ v ] . add ( u );
if ( ! PT . isPrime ( u ) && ! PT . isPrime ( v )) {
uf . union ( u , v );
}
}
long ans = 0 ;
for ( int i = 1 ; i <= n ; ++ i ) {
if ( PT . isPrime ( i )) {
long t = 0 ;
for ( int j : g [ i ] ) {
if ( ! PT . isPrime ( j )) {
long cnt = uf . size ( j );
ans += cnt ;
ans += cnt * t ;
t += cnt ;
}
}
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82 const int mx = 1e5 + 10 ;
bool prime [ mx + 1 ];
int init = []() {
for ( int i = 2 ; i <= mx ; ++ i ) prime [ i ] = true ;
for ( int i = 2 ; i <= mx ; ++ i ) {
if ( prime [ i ]) {
for ( int j = i + i ; j <= mx ; j += i ) {
prime [ j ] = false ;
}
}
}
return 0 ;
}();
class UnionFind {
public :
UnionFind ( int n ) {
p = vector < int > ( n );
size = vector < int > ( n , 1 );
iota ( p . begin (), p . end (), 0 );
}
bool unite ( int a , int b ) {
int pa = find ( a ), pb = find ( b );
if ( pa == pb ) {
return false ;
}
if ( size [ pa ] > size [ pb ]) {
p [ pb ] = pa ;
size [ pa ] += size [ pb ];
} else {
p [ pa ] = pb ;
size [ pb ] += size [ pa ];
}
return true ;
}
int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ]);
}
return p [ x ];
}
int getSize ( int x ) {
return size [ find ( x )];
}
private :
vector < int > p , size ;
};
class Solution {
public :
long long countPaths ( int n , vector < vector < int >>& edges ) {
vector < int > g [ n + 1 ];
UnionFind uf ( n + 1 );
for ( auto & e : edges ) {
int u = e [ 0 ], v = e [ 1 ];
g [ u ]. push_back ( v );
g [ v ]. push_back ( u );
if ( ! prime [ u ] && ! prime [ v ]) {
uf . unite ( u , v );
}
}
long long ans = 0 ;
for ( int i = 1 ; i <= n ; ++ i ) {
if ( prime [ i ]) {
long long t = 0 ;
for ( int j : g [ i ]) {
if ( ! prime [ j ]) {
long long cnt = uf . getSize ( j );
ans += cnt ;
ans += cnt * t ;
t += cnt ;
}
}
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82 const mx int = 1e5 + 10
var prime [ mx ] bool
func init () {
for i := 2 ; i < mx ; i ++ {
prime [ i ] = true
}
for i := 2 ; i < mx ; i ++ {
if prime [ i ] {
for j := i + i ; j < mx ; j += i {
prime [ j ] = false
}
}
}
}
type unionFind struct {
p , size [] int
}
func newUnionFind ( n int ) * unionFind {
p := make ([] int , n )
size := make ([] int , n )
for i := range p {
p [ i ] = i
size [ i ] = 1
}
return & unionFind { p , size }
}
func ( uf * unionFind ) find ( x int ) int {
if uf . p [ x ] != x {
uf . p [ x ] = uf . find ( uf . p [ x ])
}
return uf . p [ x ]
}
func ( uf * unionFind ) union ( a , b int ) bool {
pa , pb := uf . find ( a ), uf . find ( b )
if pa == pb {
return false
}
if uf . size [ pa ] > uf . size [ pb ] {
uf . p [ pb ] = pa
uf . size [ pa ] += uf . size [ pb ]
} else {
uf . p [ pa ] = pb
uf . size [ pb ] += uf . size [ pa ]
}
return true
}
func ( uf * unionFind ) getSize ( x int ) int {
return uf . size [ uf . find ( x )]
}
func countPaths ( n int , edges [][] int ) ( ans int64 ) {
uf := newUnionFind ( n + 1 )
g := make ([][] int , n + 1 )
for _ , e := range edges {
u , v := e [ 0 ], e [ 1 ]
g [ u ] = append ( g [ u ], v )
g [ v ] = append ( g [ v ], u )
if ! prime [ u ] && ! prime [ v ] {
uf . union ( u , v )
}
}
for i := 1 ; i <= n ; i ++ {
if prime [ i ] {
t := 0
for _ , j := range g [ i ] {
if ! prime [ j ] {
cnt := uf . getSize ( j )
ans += int64 ( cnt + cnt * t )
t += cnt
}
}
}
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75 const mx = 100010 ;
const prime = Array ( mx ). fill ( true );
prime [ 0 ] = prime [ 1 ] = false ;
for ( let i = 2 ; i <= mx ; ++ i ) {
if ( prime [ i ]) {
for ( let j = i + i ; j <= mx ; j += i ) {
prime [ j ] = false ;
}
}
}
class UnionFind {
p : number [];
size : number [];
constructor ( n : number ) {
this . p = Array ( n )
. fill ( 0 )
. map (( _ , i ) => i );
this . size = Array ( n ). fill ( 1 );
}
find ( x : number ) : number {
if ( this . p [ x ] !== x ) {
this . p [ x ] = this . find ( this . p [ x ]);
}
return this . p [ x ];
}
union ( a : number , b : number ) : boolean {
const [ pa , pb ] = [ this . find ( a ), this . find ( b )];
if ( pa === pb ) {
return false ;
}
if ( this . size [ pa ] > this . size [ pb ]) {
this . p [ pb ] = pa ;
this . size [ pa ] += this . size [ pb ];
} else {
this . p [ pa ] = pb ;
this . size [ pb ] += this . size [ pa ];
}
return true ;
}
getSize ( x : number ) : number {
return this . size [ this . find ( x )];
}
}
function countPaths ( n : number , edges : number [][]) : number {
const uf = new UnionFind ( n + 1 );
const g : number [][] = Array ( n + 1 )
. fill ( 0 )
. map (() => []);
for ( const [ u , v ] of edges ) {
g [ u ]. push ( v );
g [ v ]. push ( u );
if ( ! prime [ u ] && ! prime [ v ]) {
uf . union ( u , v );
}
}
let ans = 0 ;
for ( let i = 1 ; i <= n ; ++ i ) {
if ( prime [ i ]) {
let t = 0 ;
for ( let j of g [ i ]) {
if ( ! prime [ j ]) {
const cnt = uf . getSize ( j );
ans += cnt + t * cnt ;
t += cnt ;
}
}
}
}
return ans ;
}
Solution 2
Python3 Java C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 class Solution :
def countPaths ( self , n : int , edges : List [ List [ int ]]) -> int :
def mul ( x , y ):
return x * y
def dfs ( x , f , con , prime , r ):
v = [ 1 - prime [ x ], prime [ x ]]
for y in con [ x ]:
if y == f :
continue
p = dfs ( y , x , con , prime , r )
r [ 0 ] += mul ( p [ 0 ], v [ 1 ]) + mul ( p [ 1 ], v [ 0 ])
if prime [ x ]:
v [ 1 ] += p [ 0 ]
else :
v [ 0 ] += p [ 0 ]
v [ 1 ] += p [ 1 ]
return v
prime = [ True ] * ( n + 1 )
prime [ 1 ] = False
all_primes = []
for i in range ( 2 , n + 1 ):
if prime [ i ]:
all_primes . append ( i )
for x in all_primes :
temp = i * x
if temp > n :
break
prime [ temp ] = False
if i % x == 0 :
break
con = [[] for _ in range ( n + 1 )]
for e in edges :
con [ e [ 0 ]] . append ( e [ 1 ])
con [ e [ 1 ]] . append ( e [ 0 ])
r = [ 0 ]
dfs ( 1 , 0 , con , prime , r )
return r [ 0 ]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69 class Solution {
public long countPaths ( int n , int [][] edges ) {
List < Boolean > prime = new ArrayList <> ( n + 1 );
for ( int i = 0 ; i <= n ; ++ i ) {
prime . add ( true );
}
prime . set ( 1 , false );
List < Integer > all = new ArrayList <> ();
for ( int i = 2 ; i <= n ; ++ i ) {
if ( prime . get ( i )) {
all . add ( i );
}
for ( int x : all ) {
int temp = i * x ;
if ( temp > n ) {
break ;
}
prime . set ( temp , false );
if ( i % x == 0 ) {
break ;
}
}
}
List < List < Integer >> con = new ArrayList <> ( n + 1 );
for ( int i = 0 ; i <= n ; ++ i ) {
con . add ( new ArrayList <> ());
}
for ( int [] e : edges ) {
con . get ( e [ 0 ] ). add ( e [ 1 ] );
con . get ( e [ 1 ] ). add ( e [ 0 ] );
}
long [] r = { 0 };
dfs ( 1 , 0 , con , prime , r );
return r [ 0 ] ;
}
private long mul ( long x , long y ) {
return x * y ;
}
private class Pair {
int first ;
int second ;
Pair ( int first , int second ) {
this . first = first ;
this . second = second ;
}
}
private Pair dfs ( int x , int f , List < List < Integer >> con , List < Boolean > prime , long [] r ) {
Pair v = new Pair ( ! prime . get ( x ) ? 1 : 0 , prime . get ( x ) ? 1 : 0 );
for ( int y : con . get ( x )) {
if ( y == f ) continue ;
Pair p = dfs ( y , x , con , prime , r );
r [ 0 ] += mul ( p . first , v . second ) + mul ( p . second , v . first );
if ( prime . get ( x )) {
v . second += p . first ;
} else {
v . first += p . first ;
v . second += p . second ;
}
}
return v ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 class Solution {
long long mul ( long long x , long long y ) {
return x * y ;
}
pair < int , int > dfs ( int x , int f , const vector < vector < int >>& con , const vector < bool >& prime , long long & r ) {
pair < int , int > v = { ! prime [ x ], prime [ x ]};
for ( int y : con [ x ]) {
if ( y == f ) continue ;
const auto & p = dfs ( y , x , con , prime , r );
r += mul ( p . first , v . second ) + mul ( p . second , v . first );
if ( prime [ x ]) {
v . second += p . first ;
} else {
v . first += p . first ;
v . second += p . second ;
}
}
return v ;
}
public :
long long countPaths ( int n , vector < vector < int >>& edges ) {
vector < bool > prime ( n + 1 , true );
prime [ 1 ] = false ;
vector < int > all ;
for ( int i = 2 ; i <= n ; ++ i ) {
if ( prime [ i ]) {
all . push_back ( i );
}
for ( int x : all ) {
const int temp = i * x ;
if ( temp > n ) {
break ;
}
prime [ temp ] = false ;
if ( i % x == 0 ) {
break ;
}
}
}
vector < vector < int >> con ( n + 1 );
for ( const auto & e : edges ) {
con [ e [ 0 ]]. push_back ( e [ 1 ]);
con [ e [ 1 ]]. push_back ( e [ 0 ]);
}
long long r = 0 ;
dfs ( 1 , 0 , con , prime , r );
return r ;
}
};
GitHub