2090. K Radius Subarray Averages

Description

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

• For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.

 

Example 1:

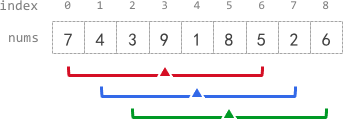
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.

Example 2:

Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input: nums = [8], k = 100000
Output: [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0.

 

Constraints:

• n == nums.length
• 1 <= n <= 105
• 0 <= nums[i], k <= 105

Solutions

Solution 1: Sliding Window

The length of a subarray with radius $k$ is $k \times 2 + 1$, so we can maintain a window of size $k \times 2 + 1$ and denote the sum of all elements in the window as $s$.

We create an answer array $\textit{ans}$ of length $n$, initially setting each element to $-1$.

Next, we traverse the array $\textit{nums}$, adding the value of $\textit{nums}[i]$ to the window sum $s$. If $i \geq k \times 2$, it means the window size is $k \times 2 + 1$, so we set $\textit{ans}[i-k] = \frac{s}{k \times 2 + 1}$. Then, we remove the value of $\textit{nums}[i - k \times 2]$ from the window sum $s$. Continue traversing the next element.

Finally, return the answer array.

The time complexity is $O(n)$, where $n$ is the length of the array $\textit{nums}$. Ignoring the space consumption of the answer array, the space complexity is $O(1)$.

Python3JavaC++GoTypeScript

class Solution:
    def getAverages(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        ans = [-1] * n
        s = 0
        for i, x in enumerate(nums):
            s += x
            if i >= k * 2:
                ans[i - k] = s // (k * 2 + 1)
                s -= nums[i - k * 2]
        return ans

class Solution {
    public int[] getAverages(int[] nums, int k) {
        int n = nums.length;
        int[] ans = new int[n];
        Arrays.fill(ans, -1);
        long s = 0;
        for (int i = 0; i < n; ++i) {
            s += nums[i];
            if (i >= k * 2) {
                ans[i - k] = (int) (s / (k * 2 + 1));
                s -= nums[i - k * 2];
            }
        }
        return ans;
    }
}

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> ans(n, -1);
        long long s = 0;
        for (int i = 0; i < n; ++i) {
            s += nums[i];
            if (i >= k * 2) {
                ans[i - k] = s / (k * 2 + 1);
                s -= nums[i - k * 2];
            }
        }
        return ans;
    }
};

func getAverages(nums []int, k int) []int {
    ans := make([]int, len(nums))
    for i := range ans {
        ans[i] = -1
    }
    s := 0
    for i, x := range nums {
        s += x
        if i >= k*2 {
            ans[i-k] = s / (k*2 + 1)
            s -= nums[i-k*2]
        }
    }
    return ans
}

function getAverages(nums: number[], k: number): number[] {
    const n = nums.length;
    const ans: number[] = Array(n).fill(-1);
    let s = 0;
    for (let i = 0; i < n; ++i) {
        s += nums[i];
        if (i >= k * 2) {
            ans[i - k] = Math.floor(s / (k * 2 + 1));
            s -= nums[i - k * 2];
        }
    }
    return ans;
}

Comments