Binary Tree
Breadth-First Search
Depth-First Search
Tree
Description
Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed) .
Example 1:
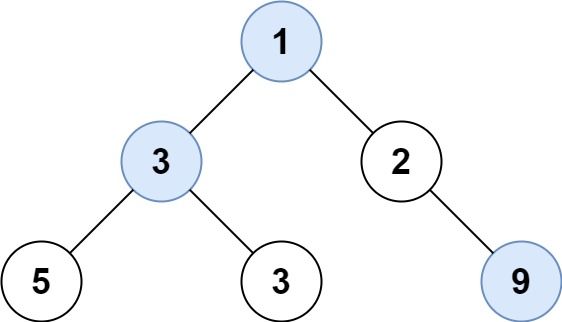
Input: root = [1,3,2,5,3,null,9]
Output: [1,3,9]
Example 2:
Input: root = [1,2,3]
Output: [1,3]
Constraints:
The number of nodes in the tree will be in the range [0, 104 ].
-231 <= Node.val <= 231 - 1
Solutions
Solution 1: BFS
We define a queue \(q\) and put the root node into the queue. Each time, we take out all the nodes of the current level from the queue, find the maximum value, and then put all the nodes of the next level into the queue until the queue is empty.
The time complexity is \(O(n)\) , and the space complexity is \(O(n)\) . Here, \(n\) is the number of nodes in the binary tree.
Python3 Java C++ Go TypeScript Rust
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def largestValues ( self , root : Optional [ TreeNode ]) -> List [ int ]:
ans = []
if root is None :
return ans
q = deque ([ root ])
while q :
x = - inf
for _ in range ( len ( q )):
node = q . popleft ()
x = max ( x , node . val )
if node . left :
q . append ( node . left )
if node . right :
q . append ( node . right )
ans . append ( x )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List < Integer > largestValues ( TreeNode root ) {
List < Integer > ans = new ArrayList <> ();
if ( root == null ) {
return ans ;
}
Deque < TreeNode > q = new ArrayDeque <> ();
q . offer ( root );
while ( ! q . isEmpty ()) {
int t = q . peek (). val ;
for ( int i = q . size (); i > 0 ; -- i ) {
TreeNode node = q . poll ();
t = Math . max ( t , node . val );
if ( node . left != null ) {
q . offer ( node . left );
}
if ( node . right != null ) {
q . offer ( node . right );
}
}
ans . add ( t );
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
vector < int > largestValues ( TreeNode * root ) {
vector < int > ans ;
if ( ! root ) {
return ans ;
}
queue < TreeNode *> q {{ root }};
while ( q . size ()) {
int x = INT_MIN ;
for ( int i = q . size (); i ; -- i ) {
TreeNode * node = q . front ();
q . pop ();
x = max ( x , node -> val );
if ( node -> left ) {
q . push ( node -> left );
}
if ( node -> right ) {
q . push ( node -> right );
}
}
ans . push_back ( x );
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func largestValues ( root * TreeNode ) ( ans [] int ) {
if root == nil {
return
}
q := [] * TreeNode { root }
for len ( q ) > 0 {
x := q [ 0 ]. Val
for i := len ( q ); i > 0 ; i -- {
node := q [ 0 ]
q = q [ 1 :]
x = max ( x , node . Val )
if node . Left != nil {
q = append ( q , node . Left )
}
if node . Right != nil {
q = append ( q , node . Right )
}
}
ans = append ( ans , x )
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function largestValues ( root : TreeNode | null ) : number [] {
const ans : number [] = [];
if ( ! root ) {
return ans ;
}
const q : TreeNode [] = [ root ];
while ( q . length ) {
const nq : TreeNode [] = [];
let x = - Infinity ;
for ( const { val , left , right } of q ) {
x = Math . max ( x , val );
if ( left ) {
nq . push ( left );
}
if ( right ) {
nq . push ( right );
}
}
ans . push ( x );
q . length = 0 ;
q . push (... nq );
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std :: cell :: RefCell ;
use std :: collections :: VecDeque ;
use std :: rc :: Rc ;
impl Solution {
pub fn largest_values ( root : Option < Rc < RefCell < TreeNode >>> ) -> Vec < i32 > {
let mut ans = Vec :: new ();
let mut q = VecDeque :: new ();
if root . is_some () {
q . push_back ( root . clone ());
}
while ! q . is_empty () {
let mut x = i32 :: MIN ;
for _ in 0 .. q . len () {
let node = q . pop_front (). unwrap ();
let node = node . as_ref (). unwrap (). borrow ();
x = x . max ( node . val );
if node . left . is_some () {
q . push_back ( node . left . clone ());
}
if node . right . is_some () {
q . push_back ( node . right . clone ());
}
}
ans . push ( x );
}
ans
}
}
Solution 2
Python3 Java C++ Go TypeScript Rust
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def largestValues ( self , root : Optional [ TreeNode ]) -> List [ int ]:
def dfs ( root , curr ):
if root is None :
return
if curr == len ( ans ):
ans . append ( root . val )
else :
ans [ curr ] = max ( ans [ curr ], root . val )
dfs ( root . left , curr + 1 )
dfs ( root . right , curr + 1 )
ans = []
dfs ( root , 0 )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private List < Integer > ans = new ArrayList <> ();
public List < Integer > largestValues ( TreeNode root ) {
dfs ( root , 0 );
return ans ;
}
private void dfs ( TreeNode root , int curr ) {
if ( root == null ) {
return ;
}
if ( curr == ans . size ()) {
ans . add ( root . val );
} else {
ans . set ( curr , Math . max ( ans . get ( curr ), root . val ));
}
dfs ( root . left , curr + 1 );
dfs ( root . right , curr + 1 );
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
vector < int > ans ;
vector < int > largestValues ( TreeNode * root ) {
dfs ( root , 0 );
return ans ;
}
void dfs ( TreeNode * root , int curr ) {
if ( ! root ) return ;
if ( curr == ans . size ())
ans . push_back ( root -> val );
else
ans [ curr ] = max ( ans [ curr ], root -> val );
dfs ( root -> left , curr + 1 );
dfs ( root -> right , curr + 1 );
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func largestValues ( root * TreeNode ) [] int {
var ans [] int
var dfs func ( * TreeNode , int )
dfs = func ( root * TreeNode , curr int ) {
if root == nil {
return
}
if curr == len ( ans ) {
ans = append ( ans , root . Val )
} else {
ans [ curr ] = max ( ans [ curr ], root . Val )
}
dfs ( root . Left , curr + 1 )
dfs ( root . Right , curr + 1 )
}
dfs ( root , 0 )
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function largestValues ( root : TreeNode | null ) : number [] {
const res = [];
const dfs = ( root : TreeNode | null , depth : number ) => {
if ( root == null ) {
return ;
}
const { val , left , right } = root ;
if ( res . length == depth ) {
res . push ( val );
} else {
res [ depth ] = Math . max ( res [ depth ], val );
}
dfs ( left , depth + 1 );
dfs ( right , depth + 1 );
};
dfs ( root , 0 );
return res ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std :: cell :: RefCell ;
use std :: rc :: Rc ;
impl Solution {
fn dfs ( root : & Option < Rc < RefCell < TreeNode >>> , depth : usize , res : & mut Vec < i32 > ) {
if root . is_none () {
return ;
}
let node = root . as_ref (). unwrap (). borrow ();
if res . len () == depth {
res . push ( node . val );
} else {
res [ depth ] = res [ depth ]. max ( node . val );
}
Self :: dfs ( & node . left , depth + 1 , res );
Self :: dfs ( & node . right , depth + 1 , res );
}
pub fn largest_values ( root : Option < Rc < RefCell < TreeNode >>> ) -> Vec < i32 > {
let mut res = Vec :: new ();
Self :: dfs ( & root , 0 , & mut res );
res
}
}
GitHub