2545. Sort the Students by Their Kth Score

Description

There is a class with m students and n exams. You are given a 0-indexed m x n integer matrix score, where each row represents one student and score[i][j] denotes the score the ith student got in the jth exam. The matrix score contains distinct integers only.

You are also given an integer k. Sort the students (i.e., the rows of the matrix) by their scores in the kth (0-indexed) exam from the highest to the lowest.

Return the matrix after sorting it.

 

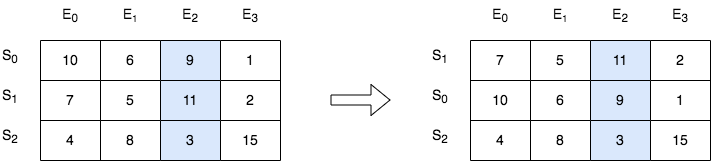
Example 1:

Input: score = [[10,6,9,1],[7,5,11,2],[4,8,3,15]], k = 2
Output: [[7,5,11,2],[10,6,9,1],[4,8,3,15]]
Explanation: In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 11 in exam 2, which is the highest score, so they got first place.
- The student with index 0 scored 9 in exam 2, which is the second highest score, so they got second place.
- The student with index 2 scored 3 in exam 2, which is the lowest score, so they got third place.

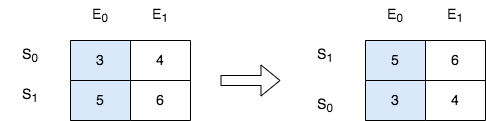
Example 2:

Input: score = [[3,4],[5,6]], k = 0
Output: [[5,6],[3,4]]
Explanation: In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 5 in exam 0, which is the highest score, so they got first place.
- The student with index 0 scored 3 in exam 0, which is the lowest score, so they got second place.

 

Constraints:

• m == score.length
• n == score[i].length
• 1 <= m, n <= 250
• 1 <= score[i][j] <= 105
• score consists of distinct integers.
• 0 <= k < n

Solutions

Solution 1: Sorting

We directly sort $\textit{score}$ in descending order based on the scores in the $k$-th column, and then return the result.

The time complexity is $O(m \times \log m)$, and the space complexity is $O(\log m)$. Here, $m$ is the number of rows in $\textit{score}$.

Python3JavaC++GoTypeScriptRust

class Solution:
    def sortTheStudents(self, score: List[List[int]], k: int) -> List[List[int]]:
        return sorted(score, key=lambda x: -x[k])

class Solution {
    public int[][] sortTheStudents(int[][] score, int k) {
        Arrays.sort(score, (a, b) -> b[k] - a[k]);
        return score;
    }
}

class Solution {
public:
    vector<vector<int>> sortTheStudents(vector<vector<int>>& score, int k) {
        ranges::sort(score, [k](const auto& a, const auto& b) { return a[k] > b[k]; });
        return score;
    }
};

func sortTheStudents(score [][]int, k int) [][]int {
    sort.Slice(score, func(i, j int) bool { return score[i][k] > score[j][k] })
    return score
}

function sortTheStudents(score: number[][], k: number): number[][] {
    return score.sort((a, b) => b[k] - a[k]);
}

impl Solution {
    pub fn sort_the_students(mut score: Vec<Vec<i32>>, k: i32) -> Vec<Vec<i32>> {
        let k = k as usize;
        score.sort_by(|a, b| b[k].cmp(&a[k]));
        score
    }
}

Comments