Skip to content

1632. Rank Transform of a Matrix

Description

Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].

The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:

  • The rank is an integer starting from 1.
  • If two elements p and q are in the same row or column, then:
    • If p < q then rank(p) < rank(q)
    • If p == q then rank(p) == rank(q)
    • If p > q then rank(p) > rank(q)
  • The rank should be as small as possible.

The test cases are generated so that answer is unique under the given rules.

 

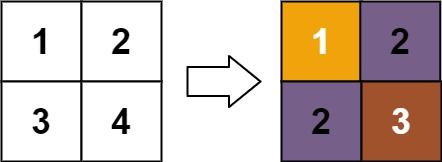
Example 1:

Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.

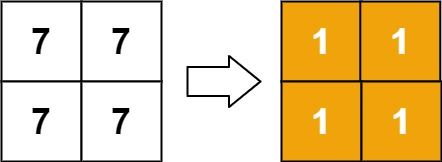
Example 2:

Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]

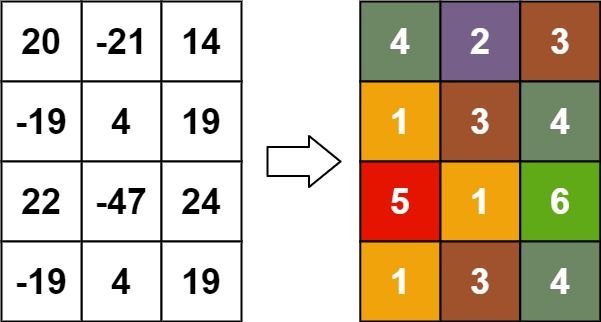
Example 3:

Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 500
  • -109 <= matrix[row][col] <= 109

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.size = [1] * n

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, a, b):
        pa, pb = self.find(a), self.find(b)
        if pa != pb:
            if self.size[pa] > self.size[pb]:
                self.p[pb] = pa
                self.size[pa] += self.size[pb]
            else:
                self.p[pa] = pb
                self.size[pb] += self.size[pa]

    def reset(self, x):
        self.p[x] = x
        self.size[x] = 1


class Solution:
    def matrixRankTransform(self, matrix: List[List[int]]) -> List[List[int]]:
        m, n = len(matrix), len(matrix[0])
        d = defaultdict(list)
        for i, row in enumerate(matrix):
            for j, v in enumerate(row):
                d[v].append((i, j))
        row_max = [0] * m
        col_max = [0] * n
        ans = [[0] * n for _ in range(m)]
        uf = UnionFind(m + n)
        for v in sorted(d):
            rank = defaultdict(int)
            for i, j in d[v]:
                uf.union(i, j + m)
            for i, j in d[v]:
                rank[uf.find(i)] = max(rank[uf.find(i)], row_max[i], col_max[j])
            for i, j in d[v]:
                ans[i][j] = row_max[i] = col_max[j] = 1 + rank[uf.find(i)]
            for i, j in d[v]:
                uf.reset(i)
                uf.reset(j + m)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
class UnionFind {
    private int[] p;
    private int[] size;

    public UnionFind(int n) {
        p = new int[n];
        size = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
            size[i] = 1;
        }
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    public void union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            if (size[pa] > size[pb]) {
                p[pb] =