Backtracking
Description
Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle .
Example 1:
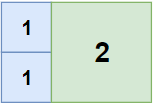
Input: n = 2, m = 3
Output: 3
Explanation: 3 squares are necessary to cover the rectangle.
2 (squares of 1x1)
1 (square of 2x2)
Example 2:
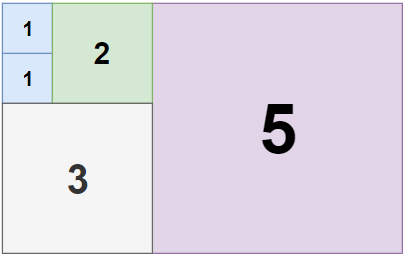
Input: n = 5, m = 8
Output: 5
Example 3:
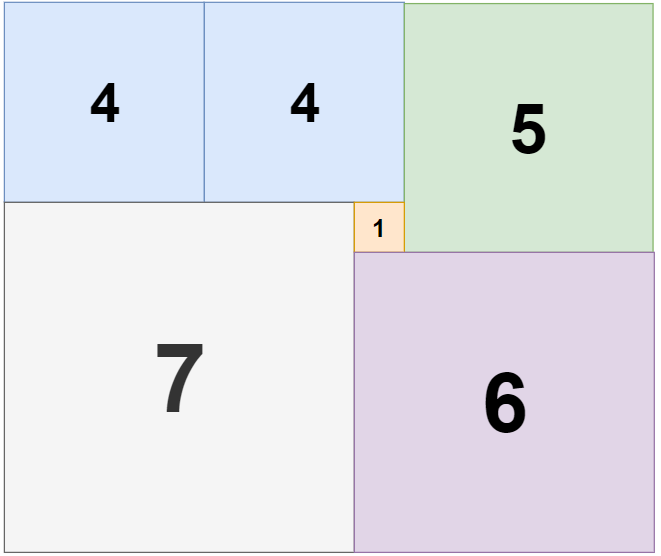
Input: n = 11, m = 13
Output: 6
Constraints:
Solutions
Solution 1: Recursive Backtracking + State Compression
We can perform recursive backtracking by position, during which we use a variable \(t\) to record the current number of tiles used.
If \(j = m\) , i.e., the \(i\) -th row has been completely filled, then we recurse to the next row, i.e., \((i + 1, 0)\) .
If \(i = n\) , it means that all positions have been filled, we update the answer and return.
If the current position \((i, j)\) has been filled, then directly recurse to the next position \((i, j + 1)\) .
Otherwise, we enumerate the maximum square side length \(w\) that the current position \((i, j)\) can fill, and fill all positions from \((i, j)\) to \((i + w - 1, j + w - 1)\) , then recurse to the next position \((i, j + w)\) . When backtracking, we need to clear all positions from \((i, j)\) to \((i + w - 1, j + w - 1)\) .
Since each position only has two states: filled or not filled, we can use an integer to represent the current state. We use an integer array \(filled\) of length \(n\) , where \(filled[i]\) represents the state of the \(i\) -th row. If the \(j\) -th bit of \(filled[i]\) is \(1\) , it means that the \(i\) -th row and the \(j\) -th column have been filled, otherwise it means not filled.
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 class Solution :
def tilingRectangle ( self , n : int , m : int ) -> int :
def dfs ( i : int , j : int , t : int ):
nonlocal ans
if j == m :
i += 1
j = 0
if i == n :
ans = t
return
if filled [ i ] >> j & 1 :
dfs ( i , j + 1 , t )
elif t + 1 < ans :
r = c = 0
for k in range ( i , n ):
if filled [ k ] >> j & 1 :
break
r += 1
for k in range ( j , m ):
if filled [ i ] >> k & 1 :
break
c += 1
mx = r if r < c else c
for w in range ( 1 , mx + 1 ):
for k in range ( w ):
filled [ i + w - 1 ] |= 1 << ( j + k )
filled [ i + k ] |= 1 << ( j + w - 1 )
dfs ( i , j + w , t + 1 )
for x in range ( i , i + mx ):
for y in range ( j , j + mx ):
filled [ x ] ^= 1 << y
ans = n * m
filled = [ 0 ] * n
dfs ( 0 , 0 , 0 )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 class Solution {
private int n ;
private int m ;
private int [] filled ;
private int ans ;
public int tilingRectangle ( int n , int m ) {
this . n = n ;
this . m = m ;
ans = n * m ;
filled = new int [ n ] ;
dfs ( 0 , 0 , 0 );
return ans ;
}
private void dfs ( int i , int j , int t ) {
if ( j == m ) {
++ i ;
j = 0 ;
}
if ( i == n ) {
ans = t ;
return ;
}
if (( filled [ i ] >> j & 1 ) == 1 ) {
dfs ( i , j + 1 , t );
} else if ( t + 1 < ans ) {
int r = 0 , c = 0 ;
for ( int k = i ; k < n ; ++ k ) {
if (( filled [ k ] >> j & 1 ) == 1 ) {
break ;
}
++ r ;
}
for ( int k = j ; k < m ; ++ k ) {
if (( filled [ i ] >> k & 1 ) == 1 ) {
break ;
}
++ c ;
}
int mx = Math . min ( r , c );
for ( int w = 1 ; w <= mx ; ++ w ) {
for ( int k = 0 ; k < w ; ++ k ) {
filled [ i + w - 1 ] |= 1 << ( j + k );
filled [ i + k ] |= 1 << ( j + w - 1 );
}
dfs ( i , j + w , t + 1 );
}
for ( int x = i ; x < i + mx ; ++ x ) {
for ( int y = j ; y < j + mx ; ++ y ) {
filled [ x ] ^= 1 << y ;
}
}
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57 class Solution {
public :
int tilingRectangle ( int n , int m ) {
memset ( filled , 0 , sizeof ( filled ));
this -> n = n ;
this -> m = m ;
ans = n * m ;
dfs ( 0 , 0 , 0 );
return ans ;
}
private :
int filled [ 13 ];
int n , m ;
int ans ;
void dfs ( int i , int j , int t ) {
if ( j == m ) {
++ i ;
j = 0 ;
}
if ( i == n ) {
ans = t ;
return ;
}
if ( filled [ i ] >> j & 1 ) {
dfs ( i , j + 1 , t );
} else if ( t + 1 < ans ) {
int r = 0 , c = 0 ;
for ( int k = i ; k < n ; ++ k ) {
if ( filled [ k ] >> j & 1 ) {
break ;
}
++ r ;
}
for ( int k = j ; k < m ; ++ k ) {
if ( filled [ i ] >> k & 1 ) {
break ;
}
++ c ;
}
int mx = min ( r , c );
for ( int w = 1 ; w <= mx ; ++ w ) {
for ( int k = 0 ; k < w ; ++ k ) {
filled [ i + w - 1 ] |= 1 << ( j + k );
filled [ i + k ] |= 1 << ( j + w - 1 );
}
dfs ( i , j + w , t + 1 );
}
for ( int x = i ; x < i + mx ; ++ x ) {
for ( int y = j ; y < j + mx ; ++ y ) {
filled [ x ] ^= 1 << y ;
}
}
}
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 func tilingRectangle ( n int , m int ) int {
ans := n * m
filled := make ([] int , n )
var dfs func ( i , j , t int )
dfs = func ( i , j , t int ) {
if j == m {
i ++
j = 0
}
if i == n {
ans = t
return
}
if filled [ i ] >> j & 1 == 1 {
dfs ( i , j + 1 , t )
} else if t + 1 < ans {
var r , c int
for k := i ; k < n ; k ++ {
if filled [ k ] >> j & 1 == 1 {
break
}
r ++
}
for k := j ; k < m ; k ++ {
if filled [ i ] >> k & 1 == 1 {
break
}
c ++
}
mx := min ( r , c )
for w := 1 ; w <= mx ; w ++ {
for k := 0 ; k < w ; k ++ {
filled [ i + w - 1 ] |= 1 << ( j + k )
filled [ i + k ] |= 1 << ( j + w - 1 )
}
dfs ( i , j + w , t + 1 )
}
for x := i ; x < i + mx ; x ++ {
for y := j ; y < j + mx ; y ++ {
filled [ x ] ^= 1 << y
}
}
}
}
dfs ( 0 , 0 , 0 )
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 function tilingRectangle ( n : number , m : number ) : number {
let ans = n * m ;
const filled : number [] = new Array ( n ). fill ( 0 );
const dfs = ( i : number , j : number , t : number ) => {
if ( j === m ) {
++ i ;
j = 0 ;
}
if ( i === n ) {
ans = t ;
return ;
}
if (( filled [ i ] >> j ) & 1 ) {
dfs ( i , j + 1 , t );
} else if ( t + 1 < ans ) {
let [ r , c ] = [ 0 , 0 ];
for ( let k = i ; k < n ; ++ k ) {
if (( filled [ k ] >> j ) & 1 ) {
break ;
}
++ r ;
}
for ( let k = j ; k < m ; ++ k ) {
if (( filled [ i ] >> k ) & 1 ) {
break ;
}
++ c ;
}
const mx = Math . min ( r , c );
for ( let w = 1 ; w <= mx ; ++ w ) {
for ( let k = 0 ; k < w ; ++ k ) {
filled [ i + w - 1 ] |= 1 << ( j + k );
filled [ i + k ] |= 1 << ( j + w - 1 );
}
dfs ( i , j + w , t + 1 );
}
for ( let x = i ; x < i + mx ; ++ x ) {
for ( let y = j ; y < j + mx ; ++ y ) {
filled [ x ] ^= 1 << y ;
}
}
}
};
dfs ( 0 , 0 , 0 );
return ans ;
}
Solution 2
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 class Solution :
def tilingRectangle ( self , n : int , m : int ) -> int :
def dfs ( i : int , j : int , t : int ):
nonlocal ans
if j == m :
i += 1
j = 0
if i == n :
ans = t
return
if filled [ i ] >> j & 1 :
dfs ( i , j + 1 , t )
elif t + 1 < ans :
r = c = 0
for k in range ( i , n ):
if filled [ k ] >> j & 1 :
break
r += 1
for k in range ( j , m ):
if filled [ i ] >> k & 1 :
break
c += 1
mx = min ( r , c )
for x in range ( i , i + mx ):
for y in range ( j , j + mx ):
filled [ x ] |= 1 << y
for w in range ( mx , 0 , - 1 ):
dfs ( i , j + w , t + 1 )
for k in range ( w ):
filled [ i + w - 1 ] ^= 1 << ( j + k )
if k < w - 1 :
filled [ i + k ] ^= 1 << ( j + w - 1 )
ans = n * m
filled = [ 0 ] * n
dfs ( 0 , 0 , 0 )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58 class Solution {
private int n ;
private int m ;
private int [] filled ;
private int ans ;
public int tilingRectangle ( int n , int m ) {
this . n = n ;
this . m = m ;
ans = n * m ;
filled = new int [ n ] ;
dfs ( 0 , 0 , 0 );
return ans ;
}
private void dfs ( int i , int j , int t ) {
if ( j == m ) {
++ i ;
j = 0 ;
}
if ( i == n ) {
ans = t ;
return ;
}
if (( filled [ i ] >> j & 1 ) == 1 ) {
dfs ( i , j + 1 , t );
} else if ( t + 1 < ans ) {
int r = 0 , c = 0 ;
for ( int k = i ; k < n ; ++ k ) {
if (( filled [ k ] >> j & 1 ) == 1 ) {
break ;
}
++ r ;
}
for ( int k = j ; k < m ; ++ k ) {
if (( filled [ i ] >> k & 1 ) == 1 ) {
break ;
}
++ c ;
}
int mx = Math . min ( r , c );
for ( int x = i ; x < i + mx ; ++ x ) {
for ( int y = j ; y < j + mx ; ++ y ) {
filled [ x ] |= 1 << y ;
}
}
for ( int w = mx ; w > 0 ; -- w ) {
dfs ( i , j + w , t + 1 );
for ( int k = 0 ; k < w ; ++ k ) {
filled [ i + w - 1 ] ^= 1 << ( j + k );
if ( k < w - 1 ) {
filled [ i + k ] ^= 1 << ( j + w - 1 );
}
}
}
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59 class Solution {
public :
int tilingRectangle ( int n , int m ) {
memset ( filled , 0 , sizeof ( filled ));
this -> n = n ;
this -> m = m ;
ans = n * m ;
dfs ( 0 , 0 , 0 );
return ans ;
}
private :
int filled [ 13 ];
int n , m ;
int ans ;
void dfs ( int i , int j , int t ) {
if ( j == m ) {
++ i ;
j = 0 ;
}
if ( i == n ) {
ans = t ;
return ;
}
if ( filled [ i ] >> j & 1 ) {
dfs ( i , j + 1 , t );
} else if ( t + 1 < ans ) {
int r = 0 , c = 0 ;
for ( int k = i ; k < n ; ++ k ) {
if ( filled [ k ] >> j & 1 ) {
break ;
}
++ r ;
}
for ( int k = j ; k < m ; ++ k ) {
if ( filled [ i ] >> k & 1 ) {
break ;
}
++ c ;
}
int mx = min ( r , c );
for ( int x = i ; x < i + mx ; ++ x ) {
for ( int y = j ; y < j + mx ; ++ y ) {
filled [ x ] |= 1 << y ;
}
}
for ( int w = mx ; w ; -- w ) {
dfs ( i , j + w , t + 1 );
for ( int k = 0 ; k < w ; ++ k ) {
filled [ i + w - 1 ] ^= 1 << ( j + k );
if ( k < w - 1 ) {
filled [ i + k ] ^= 1 << ( j + w - 1 );
}
}
}
}
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 func tilingRectangle ( n int , m int ) int {
ans := n * m
filled := make ([] int , n )
var dfs func ( i , j , t int )
dfs = func ( i , j , t int ) {
if j == m {
i ++
j = 0
}
if i == n {
ans = t
return
}
if filled [ i ] >> j & 1 == 1 {
dfs ( i , j + 1 , t )
} else if t + 1 < ans {
var r , c int
for k := i ; k < n ; k ++ {
if filled [ k ] >> j & 1 == 1 {
break
}
r ++
}
for k := j ; k < m ; k ++ {
if filled [ i ] >> k & 1 == 1 {
break
}
c ++
}
mx := min ( r , c )
for x := i ; x < i + mx ; x ++ {
for y := j ; y < j + mx ; y ++ {
filled [ x ] |= 1 << y
}
}
for w := mx ; w > 0 ; w -- {
dfs ( i , j + w , t + 1 )
for k := 0 ; k < w ; k ++ {
filled [ i + w - 1 ] ^= 1 << ( j + k )
if k < w - 1 {
filled [ i + k ] ^= 1 << ( j + w - 1 )
}
}
}
}
}
dfs ( 0 , 0 , 0 )
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48 function tilingRectangle ( n : number , m : number ) : number {
let ans = n * m ;
const filled : number [] = new Array ( n ). fill ( 0 );
const dfs = ( i : number , j : number , t : number ) => {
if ( j === m ) {
++ i ;
j = 0 ;
}
if ( i === n ) {
ans = t ;
return ;
}
if (( filled [ i ] >> j ) & 1 ) {
dfs ( i , j + 1 , t );
} else if ( t + 1 < ans ) {
let [ r , c ] = [ 0 , 0 ];
for ( let k = i ; k < n ; ++ k ) {
if (( filled [ k ] >> j ) & 1 ) {
break ;
}
++ r ;
}
for ( let k = j ; k < m ; ++ k ) {
if (( filled [ i ] >> k ) & 1 ) {
break ;
}
++ c ;
}
const mx = Math . min ( r , c );
for ( let x = i ; x < i + mx ; ++ x ) {
for ( let y = j ; y < j + mx ; ++ y ) {
filled [ x ] |= 1 << y ;
}
}
for ( let w = mx ; w > 0 ; -- w ) {
dfs ( i , j + w , t + 1 );
for ( let k = 0 ; k < w ; ++ k ) {
filled [ i + w - 1 ] ^= 1 << ( j + k );
if ( k < w - 1 ) {
filled [ i + k ] ^= 1 << ( j + w - 1 );
}
}
}
}
};
dfs ( 0 , 0 , 0 );
return ans ;
}
GitHub