994. Rotting Oranges

Description

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

 

Example 1:

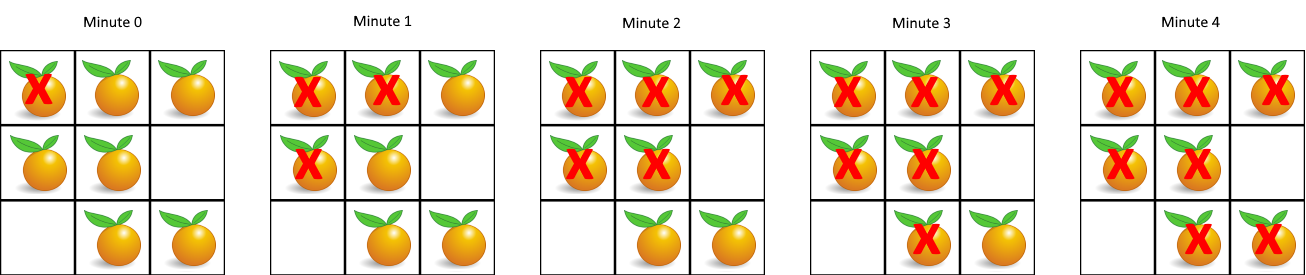
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] is 0, 1, or 2.

Solutions

Solution 1: BFS

First, we traverse the entire grid once, count the number of fresh oranges, denoted as $\textit{cnt}$, and add the coordinates of all rotten oranges to the queue $q$.

Next, we perform a breadth-first search. In each round of the search, we let all the rotten oranges in the queue rot the fresh oranges in four directions, until the queue is empty or the number of fresh oranges is $0$.

Finally, if the number of fresh oranges is $0$, we return the current round number, otherwise, we return $-1$.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Where $m$ and $n$ are the number of rows and columns of the grid, respectively.

Python3JavaC++GoTypeScriptRust

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        q = deque()
        cnt = 0
        for i, row in enumerate(grid):
            for j, x in enumerate(row):
                if x == 1:
                    cnt += 1
                elif x == 2:
                    q.append((i, j))
        dirs = (-1, 0, 1, 0, -1)
        ans = 0
        while q and cnt:
            ans += 1
            for _ in range(len(q)):
                i, j = q.popleft()
                for a, b in pairwise(dirs):
                    x, y = i + a, j + b
                    if 0 <= x < m and 0 <= y < n and grid[x][y] == 1:
                        grid[x][y] = 2
                        q.append((x, y))
                        cnt -= 1
        return -1 if cnt > 0 else ans

class Solution {
    public int orangesRotting(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        Deque<int[]> q = new ArrayDeque<>();
        int cnt = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    ++cnt;
                } else if (grid[i][j] == 2) {
                    q.offer(new int[] {i, j});
                }
            }
        }
        final int[] dirs = {-1, 0, 1, 0, -1};
        int ans = 0;
        for (; !q.isEmpty() && cnt > 0; ++ans) {
            for (int k = q.size(); k > 0; --k) {
                var p = q.poll();
                for (int d = 0; d < 4; ++d) {
                    int x = p[0] + dirs[d], y = p[1] + dirs[d + 1];
                    if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                        grid[x][y] = 2;
                        q.offer(new int[] {x, y});
                        --cnt;
                    }
                }
            }
        }
        return cnt > 0 ? -1 : ans;
    }
}

class Solution {
public:
    int orangesRotting(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        queue<pair<int, int>> q;
        int cnt = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    ++cnt;
                } else if (grid[i][j] == 2) {
                    q.emplace(i, j);
                }
            }
        }
        int ans = 0;
        const int dirs[5] = {-1, 0, 1, 0, -1};
        for (; q.size() && cnt; ++ans) {
            for (int k = q.size(); k; --k) {
                auto [i, j] = q.front();
                q.pop();
                for (int d = 0; d < 4; ++d) {
                    int x = i + dirs[d], y = j + dirs[d + 1];
                    if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                        grid[x][y] = 2;
                        q.emplace(x, y);
                        --cnt;
                    }
                }
            }
        }
        return cnt > 0 ? -1 : ans;
    }
};

func orangesRotting(grid [][]int) (ans int) {
    m, n := len(grid), len(grid[0])
    q := [][2]int{}
    cnt := 0
    for i, row := range grid {
        for j, x := range row {
            if x == 1 {
                cnt++
            } else if x == 2 {
                q = append(q, [2]int{i, j})
            }
        }
    }
    dirs := [5]int{-1, 0, 1, 0, -1}
    for ; len(q) > 0 && cnt > 0; ans++ {
        for k := len(q); k > 0; k-- {
            p := q[0]
            q = q[1:]
            for d := 0; d < 4; d++ {
                x, y := p[0]+dirs[d], p[1]+dirs[d+1]
                if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 {
                    grid[x][y] = 2
                    q = append(q, [2]int{x, y})
                    cnt--
                }
            }
        }
    }
    if cnt > 0 {
        return -1
    }
    return
}

function orangesRotting(grid: number[][]): number {
    const m: number = grid.length;
    const n: number = grid[0].length;
    const q: number[][] = [];
    let cnt: number = 0;
    for (let i: number = 0; i < m; ++i) {
        for (let j: number = 0; j < n; ++j) {
            if (grid[i][j] === 1) {
                cnt++;
            } else if (grid[i][j] === 2) {
                q.push([i, j]);
            }
        }
    }
    let ans: number = 0;
    const dirs: number[] = [-1, 0, 1, 0, -1];
    for (; q.length && cnt; ++ans) {
        const t: number[][] = [];
        for (const [i, j] of q) {
            for (let d = 0; d < 4; ++d) {
                const [x, y] = [i + dirs[d], j + dirs[d + 1]];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] === 1) {
                    grid[x][y] = 2;
                    t.push([x, y]);
                    cnt--;
                }
            }
        }
        q.splice(0, q.length, ...t);
    }
    return cnt > 0 ? -1 : ans;
}

use std::collections::VecDeque;

impl Solution {
    pub fn oranges_rotting(mut grid: Vec<Vec<i32>>) -> i32 {
        let m = grid.len();
        let n = grid[0].len();
        let mut q = VecDeque::new();
        let mut cnt = 0;

        for i in 0..m {
            for j in 0..n {
                if grid[i][j] == 1 {
                    cnt += 1;
                } else if grid[i][j] == 2 {
                    q.push_back(vec![i as i32, j as i32]);
                }
            }
        }

        let dirs: [i32; 5] = [-1, 0, 1, 0, -1];
        let mut ans = 0;

        while !q.is_empty() && cnt > 0 {
            let q_size = q.len();
            for _ in 0..q_size {
                let p = q.pop_front().unwrap();
                for d in 0..4 {
                    let x = p[0] + dirs[d];
                    let y = p[1] + dirs[d + 1];
                    if x >= 0
                        && x < (m as i32)
                        && y >= 0
                        && y < (n as i32)
                        && grid[x as usize][y as usize] == 1
                    {
                        grid[x as usize][y as usize] = 2;
                        q.push_back(vec![x, y]);
                        cnt -= 1;
                    }
                }
            }
            ans += 1;
        }

        if cnt > 0 {
            return -1;
        }

        ans
    }
}

Comments