Skip to content

941. Valid Mountain Array

Description

Given an array of integers arr, return true if and only if it is a valid mountain array.

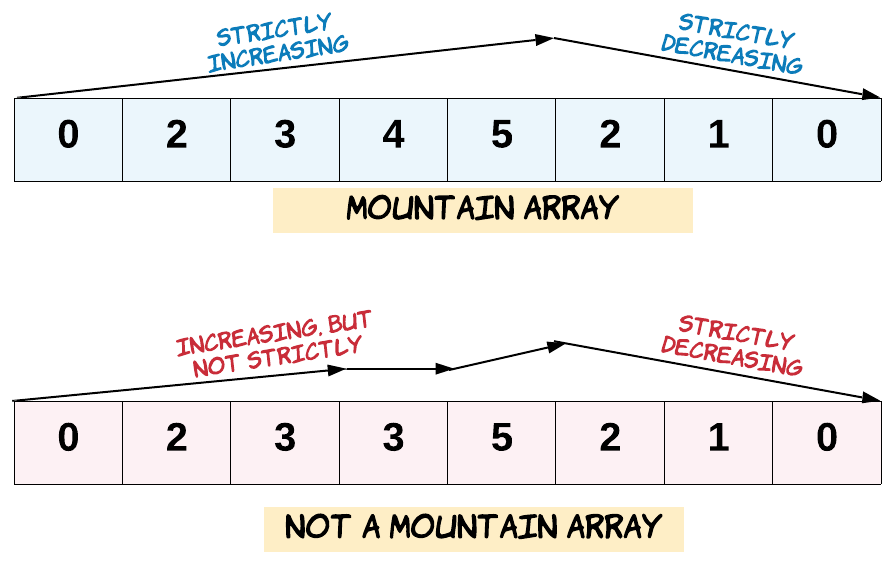
Recall that arr is a mountain array if and only if:

  • arr.length >= 3
  • There exists some i with 0 < i < arr.length - 1 such that:
    • arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
    • arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

 

Example 1:

Input: arr = [2,1]
Output: false

Example 2:

Input: arr = [3,5,5]
Output: false

Example 3:

Input: arr = [0,3,2,1]
Output: true

 

Constraints:

  • 1 <= arr.length <= 104
  • 0 <= arr[i] <= 104

Solutions

Solution 1: Two Pointers

First, we check if the length of the array is less than $3$. If it is, then it definitely is not a mountain array, so we return false directly.

Then, we use a pointer $i$ to move from the left end of the array to the right, until we find a position $i$ such that $arr[i] > arr[i + 1]$. After that, we use a pointer $j$ to move from the right end of the array to the left, until we find a position $j$ such that $arr[j] > arr[j - 1]$. If the condition $i = j$ is satisfied, then it means that the array $arr$ is a mountain array.

The time complexity is $O(n)$, where $n$ is the length of the array. The space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution:
    def validMountainArray(self, arr: List[int]) -> bool:
        n = len(arr)
        if n < 3:
            return False
        i, j = 0, n - 1
        while i + 1 < n - 1 and arr[i] < arr[i + 1]:
            i += 1
        while j - 1 > 0 and arr[j - 1] > arr[j]:
            j -= 1
        return i == j

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
    public boolean validMountainArray(int[] arr) {
        int n = arr.length;
        if (n < 3) {
            return false;
        }
        int i = 0, j = n - 1;
        while (i + 1 < n - 1 && arr[i] < arr[i + 1]) {
            ++i;
        }
        while (j - 1 > 0 && arr[j - 1] > arr[j]) {
            --j;
        }
        return i == j;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool validMountainArray(vector<int>& arr) {
        int n = arr.size();
        if (n < 3) {
            return false;
        }
        int i = 0, j = n - 1;
        while (i + 1 < n - 1 && arr[i] < arr[i + 1]) {
            ++i;
        }
        while (j - 1 > 0 && arr[j - 1] > arr[j]) {
            --j;
        }
        return i == j;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
func validMountainArray(arr []int) bool {
    n := len(arr)
    if n < 3 {
        return false
    }
    i, j := 0, n-1
    for i+1 < n-1 && arr[i] < arr[i+1] {
        i++
    }
    for j-1 > 0 && arr[j-1] > arr[j] {
        j--
    }
    return i == j
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
function validMountainArray(arr: number[]): boolean {
    const n = arr.length;
    if (n < 3) {
        return false;
    }
    let [i, j] = [0, n - 1];
    while (i + 1 < n - 1 && arr[i] < arr[i + 1]) {
        i++;
    }
    while (j - 1 > 0 && arr[j] < arr[j - 1]) {
        j--;
    }
    return i === j;
}

Comments